Question Number 185774 by cherokeesay last updated on 27/Jan/23
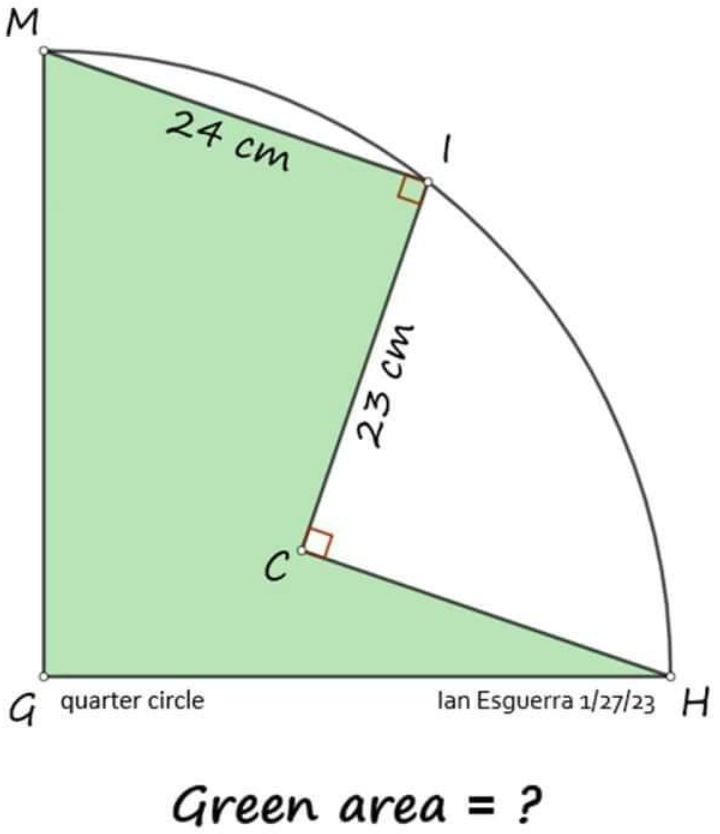
Answered by HeferH last updated on 27/Jan/23
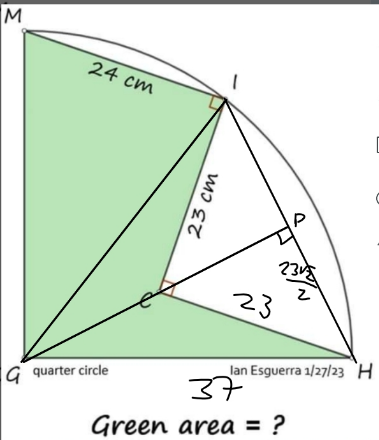
Commented by HeferH last updated on 27/Jan/23
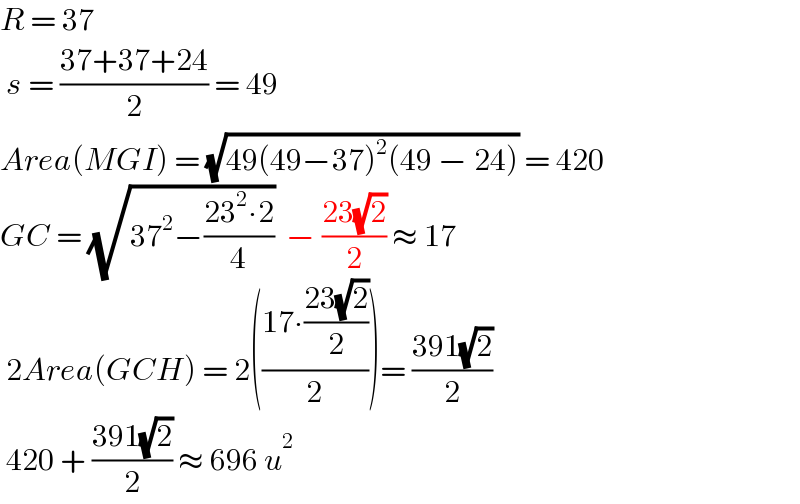
$${R}\:=\:\mathrm{37}\: \\ $$$$\:{s}\:=\:\frac{\mathrm{37}+\mathrm{37}+\mathrm{24}}{\mathrm{2}}\:=\:\mathrm{49} \\ $$$${Area}\left({MGI}\right)\:=\:\sqrt{\mathrm{49}\left(\mathrm{49}−\mathrm{37}\right)^{\mathrm{2}} \left(\mathrm{49}\:−\:\mathrm{24}\right)}\:=\:\mathrm{420} \\ $$$${GC}\:=\:\sqrt{\mathrm{37}^{\mathrm{2}} −\frac{\mathrm{23}^{\mathrm{2}} \centerdot\mathrm{2}}{\mathrm{4}}}\:\:−\:\frac{\mathrm{23}\sqrt{\mathrm{2}}}{\mathrm{2}}\:\approx\:\mathrm{17}\: \\ $$$$\:\mathrm{2}{Area}\left({GCH}\right)\:=\:\mathrm{2}\left(\frac{\mathrm{17}\centerdot\frac{\mathrm{23}\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{2}}\right)=\:\frac{\mathrm{391}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\:\mathrm{420}\:+\:\frac{\mathrm{391}\sqrt{\mathrm{2}}}{\mathrm{2}}\:\approx\:\mathrm{696}\:{u}^{\mathrm{2}} \\ $$
Commented by HeferH last updated on 27/Jan/23
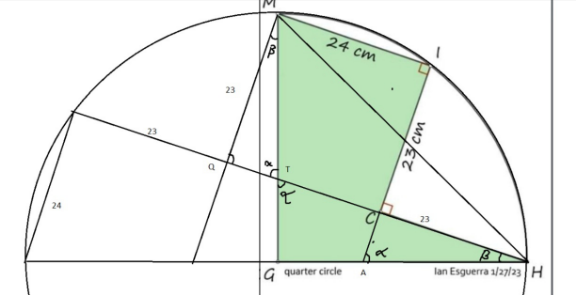
Commented by mr W last updated on 27/Jan/23
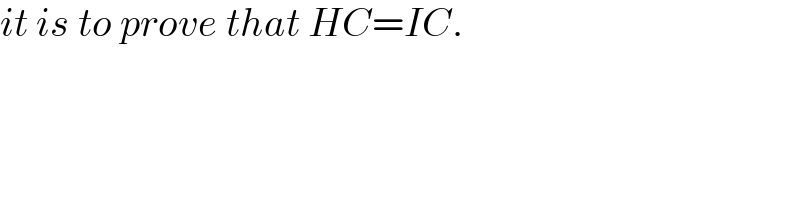
$${it}\:{is}\:{to}\:{prove}\:{that}\:{HC}={IC}. \\ $$
Commented by HeferH last updated on 27/Jan/23
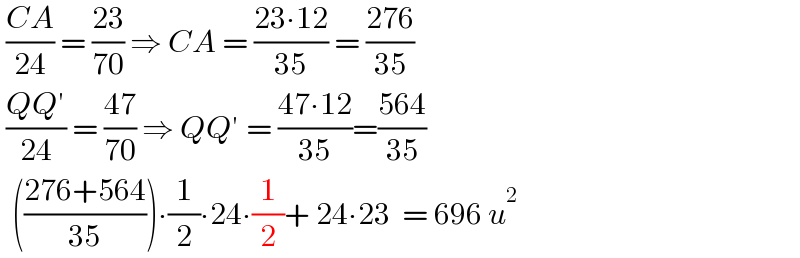
$$\:\frac{{CA}}{\mathrm{24}}\:=\:\frac{\mathrm{23}}{\mathrm{70}}\:\Rightarrow\:{CA}\:=\:\frac{\mathrm{23}\centerdot\mathrm{12}}{\mathrm{35}}\:=\:\frac{\mathrm{276}}{\mathrm{35}} \\ $$$$\:\frac{{QQ}'}{\mathrm{24}}\:=\:\frac{\mathrm{47}}{\mathrm{70}}\:\Rightarrow\:{QQ}'\:=\:\frac{\mathrm{47}\centerdot\mathrm{12}}{\mathrm{35}}=\frac{\mathrm{564}}{\mathrm{35}} \\ $$$$\:\:\left(\frac{\mathrm{276}+\mathrm{564}}{\mathrm{35}}\right)\centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot\mathrm{24}\centerdot\frac{\mathrm{1}}{\mathrm{2}}+\:\mathrm{24}\centerdot\mathrm{23}\:\:=\:\mathrm{696}\:{u}^{\mathrm{2}} \\ $$
Commented by HeferH last updated on 27/Jan/23

$${yes} \\ $$
Answered by mr W last updated on 27/Jan/23

Commented by mr W last updated on 27/Jan/23

$${a}=\mathrm{24} \\ $$$${b}=\mathrm{23} \\ $$$${c}=? \\ $$$$\mathrm{sin}\:\alpha=\frac{{b}}{\:\sqrt{\mathrm{2}}{R}}=\frac{\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }}{\mathrm{2}{R}} \\ $$$$\sqrt{\mathrm{2}}{b}=\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\Rightarrow{b}^{\mathrm{2}} ={c}^{\mathrm{2}} \:\Rightarrow{c}={b}\:\checkmark \\ $$$$\left(\sqrt{\mathrm{2}}{R}\right)^{\mathrm{2}} =\left({a}+{c}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{2}{b}\left({a}+{b}\right) \\ $$$$\Rightarrow{R}=\sqrt{\frac{{a}^{\mathrm{2}} +\mathrm{2}{b}\left({a}+{b}\right)}{\mathrm{2}}} \\ $$$$\:\:\:\:=\sqrt{\frac{\mathrm{24}^{\mathrm{2}} +\mathrm{2}×\mathrm{23}×\left(\mathrm{24}+\mathrm{23}\right)}{\mathrm{2}}}=\mathrm{37} \\ $$$${green}=\frac{{a}}{\mathrm{2}}\sqrt{{R}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}+\frac{\sqrt{\mathrm{2}}{b}}{\mathrm{2}}\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{2}}}−\frac{{b}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:=\mathrm{12}×\mathrm{58}=\mathrm{696} \\ $$
