Question Number 185805 by Rupesh123 last updated on 27/Jan/23

Answered by MJS_new last updated on 28/Jan/23
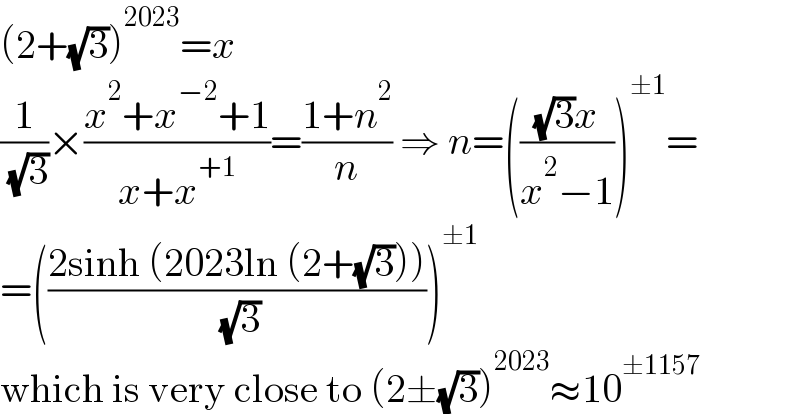
$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2023}} ={x} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}×\frac{{x}^{\mathrm{2}} +{x}^{−\mathrm{2}} +\mathrm{1}}{{x}+{x}^{+\mathrm{1}} }=\frac{\mathrm{1}+{n}^{\mathrm{2}} }{{n}}\:\Rightarrow\:{n}=\left(\frac{\sqrt{\mathrm{3}}{x}}{{x}^{\mathrm{2}} −\mathrm{1}}\right)^{\pm\mathrm{1}} = \\ $$$$=\left(\frac{\mathrm{2sinh}\:\left(\mathrm{2023ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\right)}{\:\sqrt{\mathrm{3}}}\right)^{\pm\mathrm{1}} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{very}\:\mathrm{close}\:\mathrm{to}\:\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\right)^{\mathrm{2023}} \approx\mathrm{10}^{\pm\mathrm{1157}} \\ $$
Answered by manxsol last updated on 28/Jan/23
![(2+(√3))^2 =7+(√(48)) a=2+(√3) a^2 =7+(√(48)) (1/( (√3)))[(((a^(2023) )^2 +(1/((a^(2023) )^2 ))+1)/(a^(2023) −(1/a^(2023) )))]=n+(1/n) p=a^(2023) (1/( (√(3 )) ))[((p^2 +(1/p^2 )+1)/(p−(1/p)))]=n+(1/n) (1/( (√3)))[(((p−(1/p))^2 +3)/(p−(1/p)))]=n+(1/n) (1/( (√3)))[(p−(1/p))+(3/((p−(1/p))))]=n+(1/n) (((p−(1/p)))/( (√3)))+(1/(((p−(1/p)))/( (√3))))=n+(1/n) n_1 =(a^(2023) −(1/a^(2023) ))(1/( (√3))) n_2 =((√3)/((a^(2023) −(1/a^(2023) )))) z=a^(2023) z=(2+(√3))^(2023) logz=2023log(2+(√3)) z=10^(1157.049889) (1/z)=10^(−1157.049889) ≈0 n_1 =(1/( (√3)))10^(1157.049) n_2 =(√3)10^(−1157.048)](https://www.tinkutara.com/question/Q185813.png)
$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{7}+\sqrt{\mathrm{48}} \\ $$$${a}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$${a}^{\mathrm{2}} =\mathrm{7}+\sqrt{\mathrm{48}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left[\frac{\left({a}^{\mathrm{2023}} \right)^{\mathrm{2}} +\frac{\mathrm{1}}{\left({a}^{\mathrm{2023}} \right)^{\mathrm{2}} }+\mathrm{1}}{{a}^{\mathrm{2023}} −\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }}\right]={n}+\frac{\mathrm{1}}{{n}} \\ $$$${p}={a}^{\mathrm{2023}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}\:}\:}\left[\frac{{p}^{\mathrm{2}} +\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\mathrm{1}}{{p}−\frac{\mathrm{1}}{{p}}}\right]={n}+\frac{\mathrm{1}}{{n}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left[\frac{\left({p}−\frac{\mathrm{1}}{{p}}\right)^{\mathrm{2}} +\mathrm{3}}{{p}−\frac{\mathrm{1}}{{p}}}\right]={n}+\frac{\mathrm{1}}{{n}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left[\left({p}−\frac{\mathrm{1}}{{p}}\right)+\frac{\mathrm{3}}{\left({p}−\frac{\mathrm{1}}{{p}}\right)}\right]={n}+\frac{\mathrm{1}}{{n}} \\ $$$$\frac{\left({p}−\frac{\mathrm{1}}{{p}}\right)}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\frac{\left({p}−\frac{\mathrm{1}}{{p}}\right)}{\:\sqrt{\mathrm{3}}}}={n}+\frac{\mathrm{1}}{{n}} \\ $$$${n}_{\mathrm{1}} =\left({a}^{\mathrm{2023}} −\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }\right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${n}_{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\left({a}^{\mathrm{2023}} −\frac{\mathrm{1}}{{a}^{\mathrm{2023}} }\right)} \\ $$$${z}={a}^{\mathrm{2023}} \\ $$$${z}=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2023}} \\ $$$${logz}=\mathrm{2023}{log}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$${z}=\mathrm{10}^{\mathrm{1157}.\mathrm{049889}} \\ $$$$\frac{\mathrm{1}}{{z}}=\mathrm{10}^{−\mathrm{1157}.\mathrm{049889}} \approx\mathrm{0} \\ $$$${n}_{\mathrm{1}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{10}^{\mathrm{1157}.\mathrm{049}} \\ $$$${n}_{\mathrm{2}} =\sqrt{\mathrm{3}}\mathrm{10}^{−\mathrm{1157}.\mathrm{048}} \\ $$
