Question Number 185816 by mr W last updated on 28/Jan/23

Commented by mr W last updated on 28/Jan/23
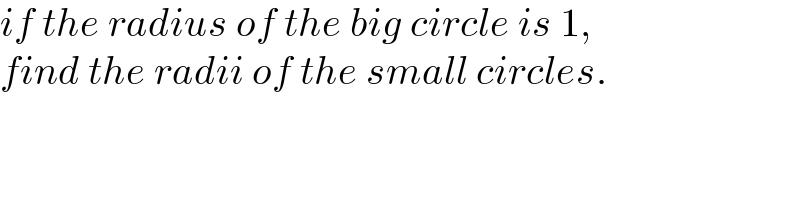
$${if}\:{the}\:{radius}\:{of}\:{the}\:{big}\:{circle}\:{is}\:\mathrm{1}, \\ $$$${find}\:{the}\:{radii}\:{of}\:{the}\:{small}\:{circles}. \\ $$
Answered by mr W last updated on 28/Jan/23
Commented by mr W last updated on 28/Jan/23
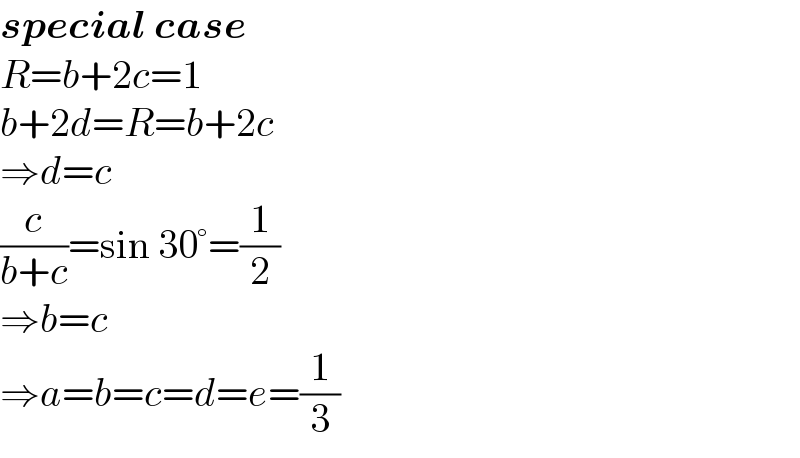
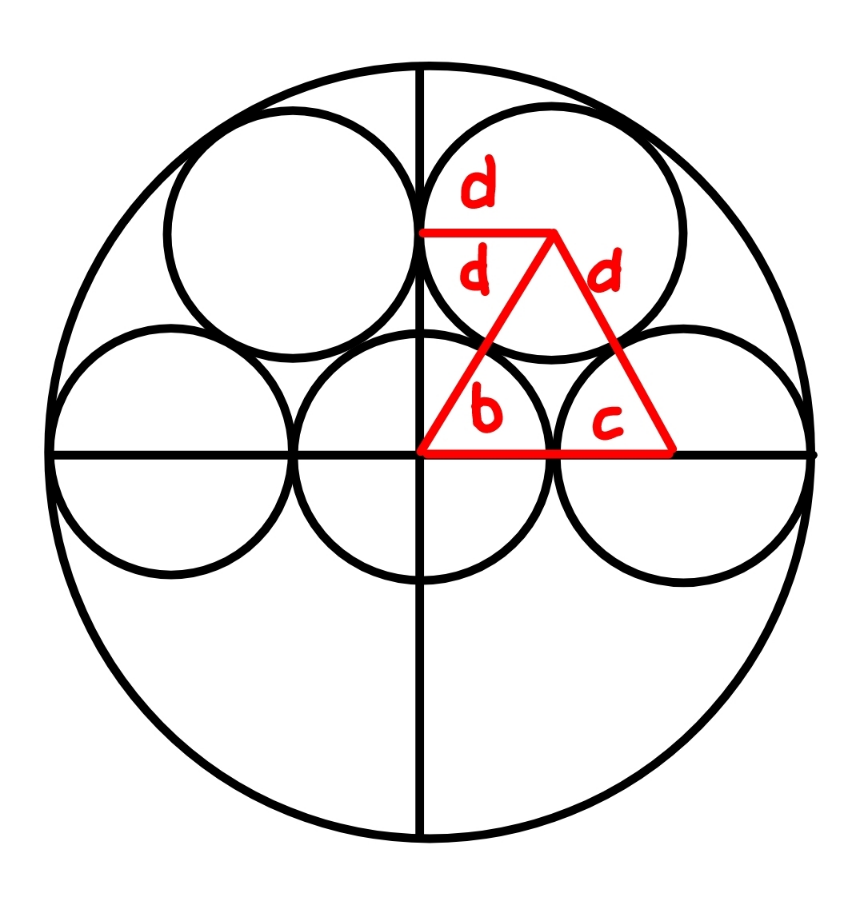
$$\boldsymbol{{special}}\:\boldsymbol{{case}} \\ $$$${R}={b}+\mathrm{2}{c}=\mathrm{1} \\ $$$${b}+\mathrm{2}{d}={R}={b}+\mathrm{2}{c} \\ $$$$\Rightarrow{d}={c} \\ $$$$\frac{{c}}{{b}+{c}}=\mathrm{sin}\:\mathrm{30}°=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{b}={c} \\ $$$$\Rightarrow{a}={b}={c}={d}={e}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by ajfour last updated on 28/Jan/23
![E[−(1−e)cos θ, (1−e)sin θ] D[(1−d)cos φ, (1−d)sin φ] {1−a−(1−e)cos θ}^2 +(1−e)^2 sin^2 θ =(a+e)^2 ⇒ (1−a)^2 −2(1−a)(1−e)cos θ =(a+e)^2 −(1−e)^2 ⇒ cos θ=((1−a−e−ae)/(1−a−e+ae)) similarly cos φ=((1−c−d−cd)/(1−c−d+cd)) ...](https://www.tinkutara.com/question/Q185827.png)
$${E}\left[−\left(\mathrm{1}−{e}\right)\mathrm{cos}\:\theta,\:\left(\mathrm{1}−{e}\right)\mathrm{sin}\:\theta\right] \\ $$$${D}\left[\left(\mathrm{1}−{d}\right)\mathrm{cos}\:\phi,\:\left(\mathrm{1}−{d}\right)\mathrm{sin}\:\phi\right] \\ $$$$\left\{\mathrm{1}−{a}−\left(\mathrm{1}−{e}\right)\mathrm{cos}\:\theta\right\}^{\mathrm{2}} +\left(\mathrm{1}−{e}\right)^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:=\left({a}+{e}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\left(\mathrm{1}−{a}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−{a}\right)\left(\mathrm{1}−{e}\right)\mathrm{cos}\:\theta \\ $$$$\:\:\:\:=\left({a}+{e}\right)^{\mathrm{2}} −\left(\mathrm{1}−{e}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta=\frac{\mathrm{1}−{a}−{e}−{ae}}{\mathrm{1}−{a}−{e}+{ae}} \\ $$$${similarly} \\ $$$$\:\:\:\mathrm{cos}\:\phi=\frac{\mathrm{1}−{c}−{d}−{cd}}{\mathrm{1}−{c}−{d}+{cd}} \\ $$$$… \\ $$
Answered by mr W last updated on 29/Jan/23

