Question Number 185851 by Mingma last updated on 28/Jan/23

Commented by Mingma last updated on 28/Jan/23
Diameter in relation to a,b,c ?
Answered by mr W last updated on 28/Jan/23
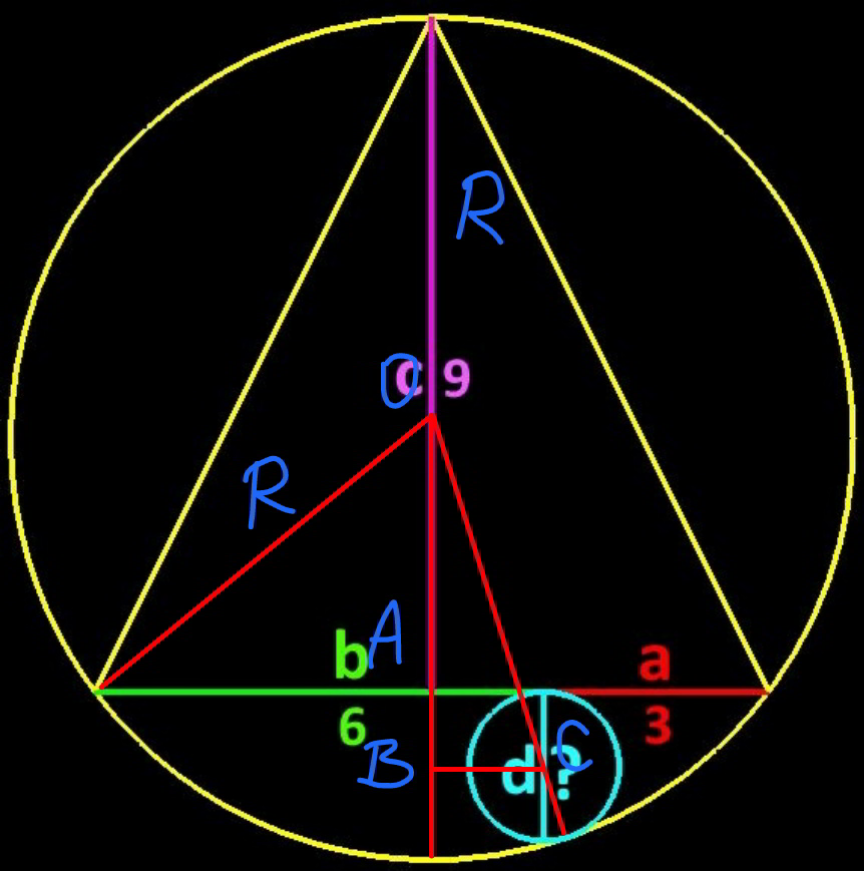
Commented by mr W last updated on 28/Jan/23
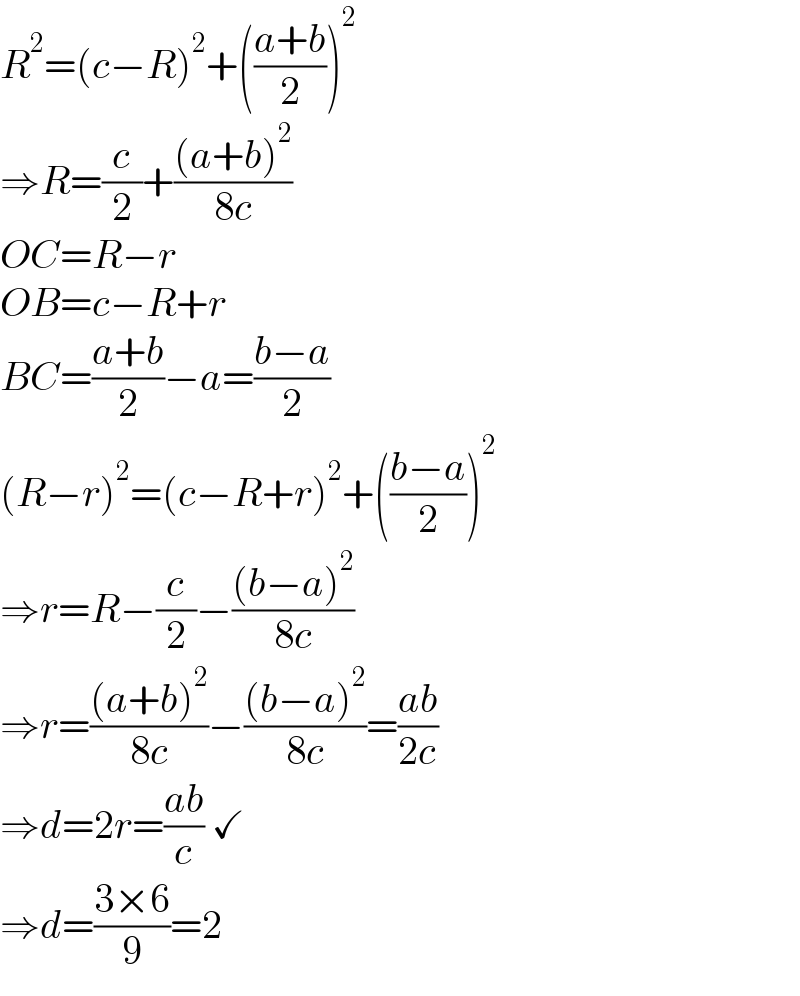
$${R}^{\mathrm{2}} =\left({c}−{R}\right)^{\mathrm{2}} +\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{{c}}{\mathrm{2}}+\frac{\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{8}{c}} \\ $$$${OC}={R}−{r} \\ $$$${OB}={c}−{R}+{r} \\ $$$${BC}=\frac{{a}+{b}}{\mathrm{2}}−{a}=\frac{{b}−{a}}{\mathrm{2}} \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} =\left({c}−{R}+{r}\right)^{\mathrm{2}} +\left(\frac{{b}−{a}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{r}={R}−\frac{{c}}{\mathrm{2}}−\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{8}{c}} \\ $$$$\Rightarrow{r}=\frac{\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{8}{c}}−\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{8}{c}}=\frac{{ab}}{\mathrm{2}{c}} \\ $$$$\Rightarrow{d}=\mathrm{2}{r}=\frac{{ab}}{{c}}\:\checkmark \\ $$$$\Rightarrow{d}=\frac{\mathrm{3}×\mathrm{6}}{\mathrm{9}}=\mathrm{2} \\ $$
