Question Number 185907 by Mingma last updated on 29/Jan/23
Answered by HeferH last updated on 29/Jan/23
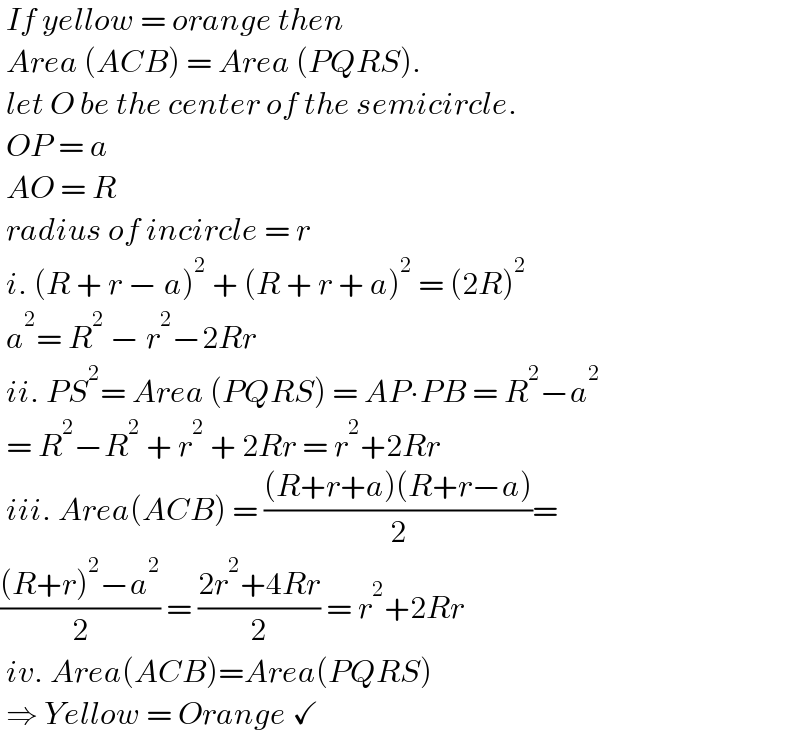
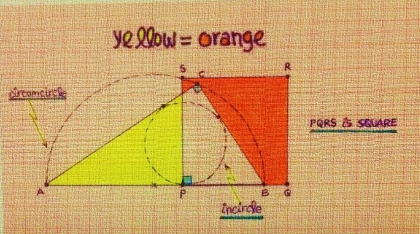
$$\:{If}\:{yellow}\:=\:{orange}\:{then}\: \\ $$$$\:{Area}\:\left({ACB}\right)\:=\:{Area}\:\left({PQRS}\right). \\ $$$$\:{let}\:{O}\:{be}\:{the}\:{center}\:{of}\:{the}\:{semicircle}. \\ $$$$\:{OP}\:=\:{a} \\ $$$$\:{AO}\:=\:{R} \\ $$$$\:{radius}\:{of}\:{incircle}\:=\:{r} \\ $$$$\:{i}.\:\left({R}\:+\:{r}\:−\:{a}\right)^{\mathrm{2}} \:+\:\left({R}\:+\:{r}\:+\:{a}\right)^{\mathrm{2}} \:=\:\left(\mathrm{2}{R}\right)^{\mathrm{2}} \\ $$$$\:{a}^{\mathrm{2}} =\:{R}^{\mathrm{2}} \:−\:{r}^{\mathrm{2}} −\mathrm{2}{Rr} \\ $$$$\:{ii}.\:{PS}^{\mathrm{2}} =\:{Area}\:\left({PQRS}\right)\:=\:{AP}\centerdot{PB}\:=\:{R}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$$\:=\:{R}^{\mathrm{2}} −{R}^{\mathrm{2}} \:+\:{r}^{\mathrm{2}} \:+\:\mathrm{2}{Rr}\:=\:{r}^{\mathrm{2}} +\mathrm{2}{Rr} \\ $$$$\:{iii}.\:{Area}\left({ACB}\right)\:=\:\frac{\left({R}+{r}+{a}\right)\left({R}+{r}−{a}\right)}{\mathrm{2}}= \\ $$$$\frac{\left({R}+{r}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}}\:=\:\frac{\mathrm{2}{r}^{\mathrm{2}} +\mathrm{4}{Rr}}{\mathrm{2}}\:=\:{r}^{\mathrm{2}} +\mathrm{2}{Rr} \\ $$$$\:{iv}.\:{Area}\left({ACB}\right)={Area}\left({PQRS}\right)\: \\ $$$$\:\Rightarrow\:{Yellow}\:=\:{Orange}\:\checkmark \\ $$
