Menu Close

Question-185924

Tinku Tara 0 Comments
Pin




Question Number 185924 by Mingma last updated on 29/Jan/23
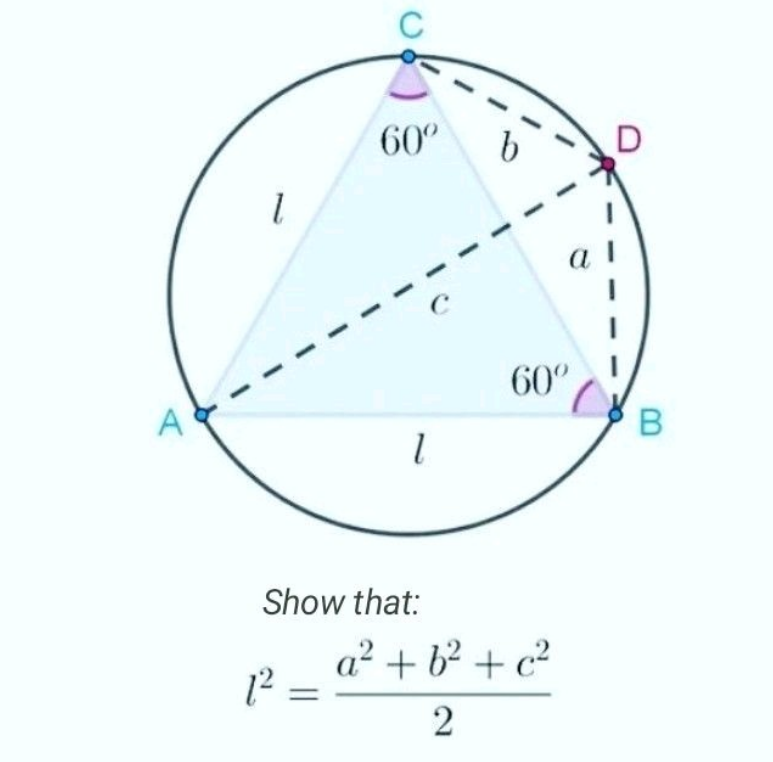
Answered by HeferH last updated on 29/Jan/23
Commented by HeferH last updated on 30/Jan/23
i. ((DE)/b) = (a/c) ⇒ DE = ((ab)/c) ((CE)/l) = (b/c) ⇒ CE = ((bl)/c) ((CD)/(CE)) = ((DB)/(EB)) ⇒ (b/((bl)/c)) = (a/(EB)) ⇒ EB = ((al)/c) ii. CE + EB = CB ⇒ ((bl)/c) + ((al)/c) = l a + b = c a^2 + b^2 + 2ab = c^2 iii. CE∙EB = AE∙ED ⇒ ((abl^2 )/c^2 ) = (((c^2 −ab)ab)/c^2 ) c^2 −l^2 = ab iv. a^2 + b^2 + 2ab = c^2 a^2 + b^2 + 2(c^2 −l^2 ) = c^2 a^2 + b^2 +2c^2 −2l^2 = c^2 l^2 = ((a^2 + b^2 + c^2 )/2)
$$\:{i}.\:\frac{{DE}}{{b}}\:=\:\frac{{a}}{{c}}\:\Rightarrow\:{DE}\:=\:\frac{{ab}}{{c}} \\ $$$$\:\frac{{CE}}{{l}}\:=\:\frac{{b}}{{c}}\:\:\Rightarrow\:\:{CE}\:=\:\frac{{bl}}{{c}}\: \\ $$$$\:\frac{{CD}}{{CE}}\:=\:\frac{{DB}}{{EB}}\:\Rightarrow\:\frac{{b}}{\frac{{bl}}{{c}}}\:=\:\frac{{a}}{{EB}}\:\Rightarrow\:{EB}\:=\:\frac{{al}}{{c}} \\ $$$$\:{ii}.\:{CE}\:+\:{EB}\:=\:{CB}\:\Rightarrow \\ $$$$\:\frac{{bl}}{{c}}\:+\:\frac{{al}}{{c}}\:=\:{l}\: \\ $$$$\:{a}\:+\:{b}\:=\:{c}\: \\ $$$$\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:+\:\mathrm{2}{ab}\:=\:{c}^{\mathrm{2}} \\ $$$$\:{iii}.\:{CE}\centerdot{EB}\:=\:{AE}\centerdot{ED}\:\Rightarrow\:\:\frac{{abl}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\:=\:\frac{\left({c}^{\mathrm{2}} −{ab}\right){ab}}{{c}^{\mathrm{2}} } \\ $$$$\:{c}^{\mathrm{2}} −{l}^{\mathrm{2}} \:\:=\:{ab}\: \\ $$$$\:{iv}.\:\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:+\:\mathrm{2}{ab}\:=\:{c}^{\mathrm{2}} \\ $$$$\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:+\:\mathrm{2}\left({c}^{\mathrm{2}} −{l}^{\mathrm{2}} \right)\:=\:{c}^{\mathrm{2}} \\ $$$$\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:+\mathrm{2}{c}^{\mathrm{2}} −\mathrm{2}{l}^{\mathrm{2}} =\:{c}^{\mathrm{2}} \\ $$$$\:{l}^{\mathrm{2}} \:=\:\frac{{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:+\:{c}^{\mathrm{2}} }{\mathrm{2}}\: \\ $$
Answered by mr W last updated on 30/Jan/23
l^2 =a^2 +b^2 +ab ...(i) l^2 =b^2 +c^2 −bc ...(ii) l^2 =a^2 +c^2 −ac ...(iii) (ii)−(iii): (a−b)c=(a−b)(a+b) ⇒c=a+b 2×(i): 2l^2 =a^2 +b^2 +a^2 +b^2 +2ab=a^2 +b^2 +(a+b)^2 2l^2 =a^2 +b^2 +c^2 ⇒l^2 =((a^2 +b^2 +c^2 )/2)
$${l}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\:\:\:…\left({i}\right) \\ $$$${l}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{bc}\:\:\:…\left({ii}\right) \\ $$$${l}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ac}\:\:\:…\left({iii}\right) \\ $$$$\left({ii}\right)−\left({iii}\right): \\ $$$$\left({a}−{b}\right){c}=\left({a}−{b}\right)\left({a}+{b}\right) \\ $$$$\Rightarrow{c}={a}+{b} \\ $$$$\mathrm{2}×\left({i}\right): \\ $$$$\mathrm{2}{l}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{l}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$$\Rightarrow{l}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *