Question Number 185953 by ajfour last updated on 30/Jan/23
Commented by ajfour last updated on 30/Jan/23

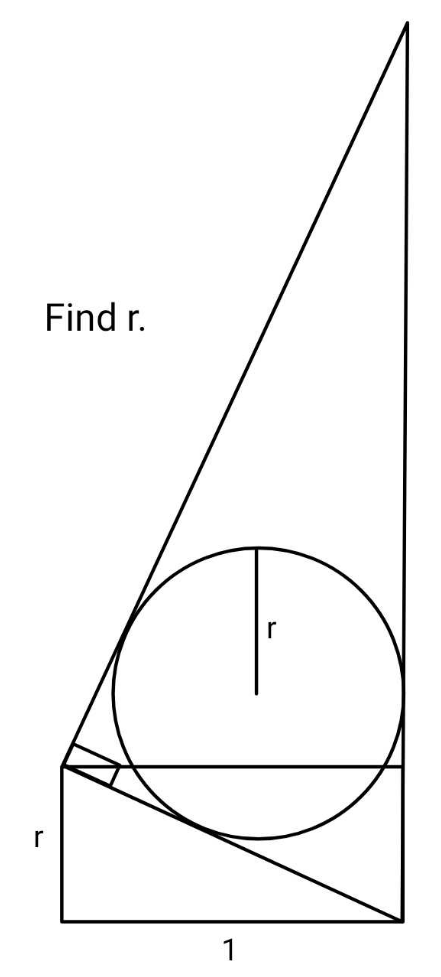
$${Would}\:{it}\:{be}\:{r}\approx\mathrm{0}.\mathrm{432}\:? \\ $$
Commented by TUN last updated on 30/Jan/23
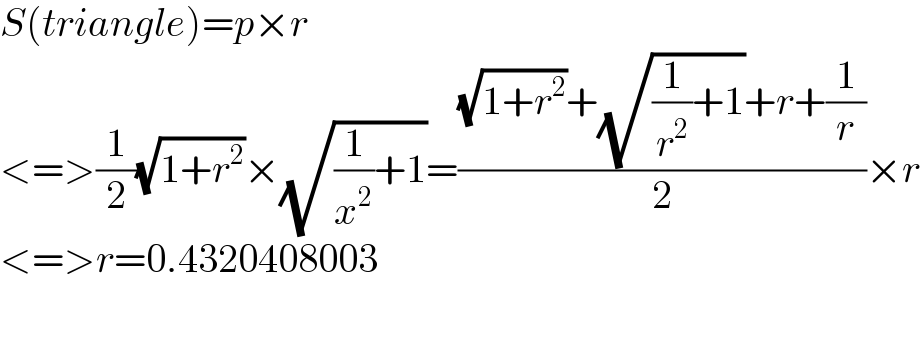
$${S}\left({triangle}\right)={p}×{r} \\ $$$$<=>\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+{r}^{\mathrm{2}} }×\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}=\frac{\sqrt{\mathrm{1}+{r}^{\mathrm{2}} }+\sqrt{\frac{\mathrm{1}}{{r}^{\mathrm{2}} }+\mathrm{1}}+{r}+\frac{\mathrm{1}}{{r}}}{\mathrm{2}}×{r} \\ $$$$<=>{r}=\mathrm{0}.\mathrm{4320408003} \\ $$$$ \\ $$
Commented by ajfour last updated on 30/Jan/23
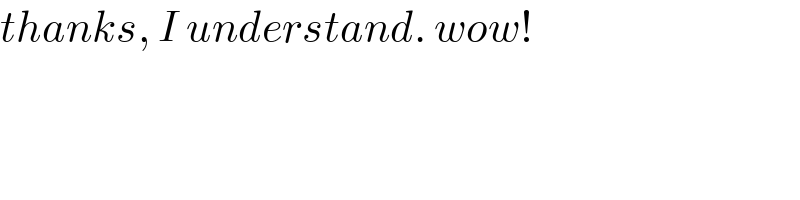
$${thanks},\:{I}\:{understand}.\:{wow}! \\ $$
Answered by mr W last updated on 30/Jan/23
Commented by mr W last updated on 30/Jan/23
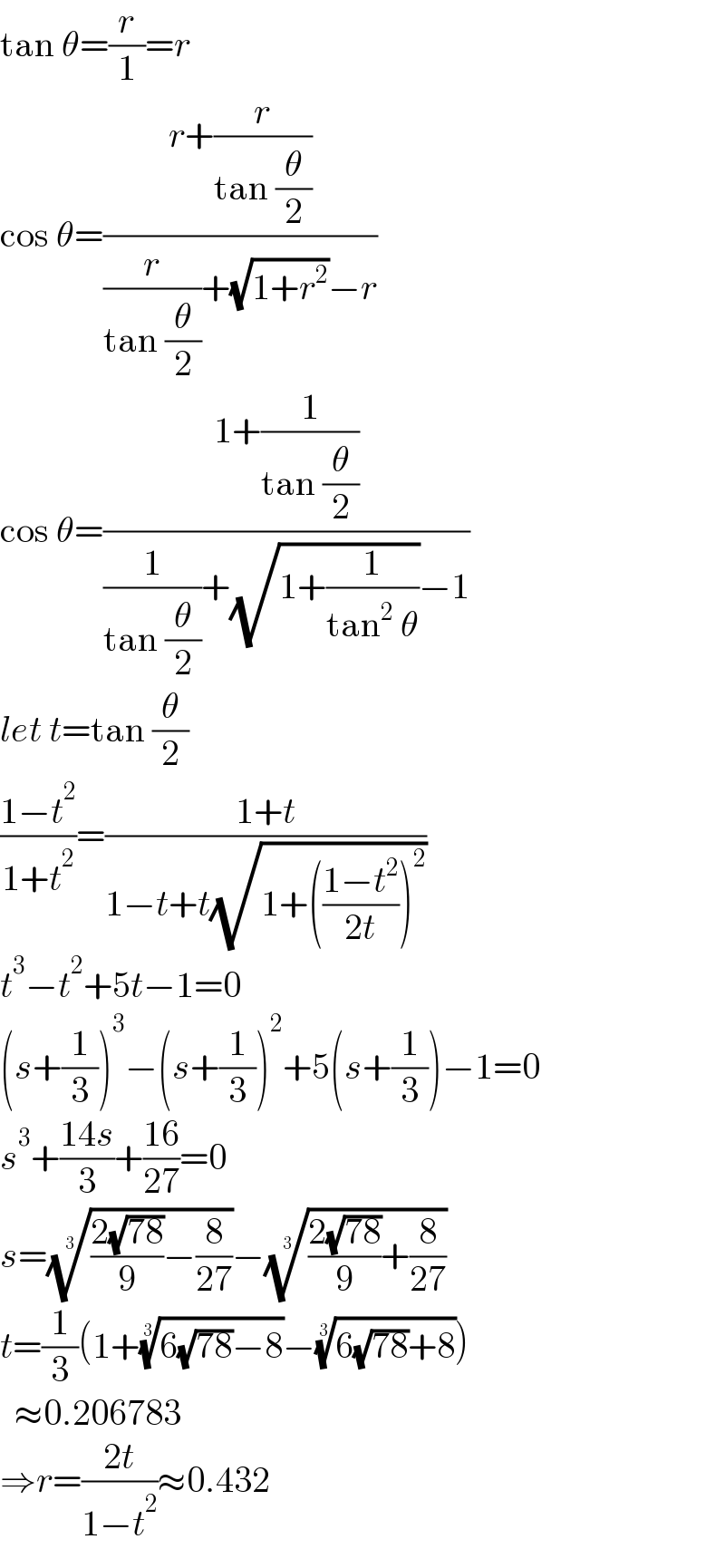
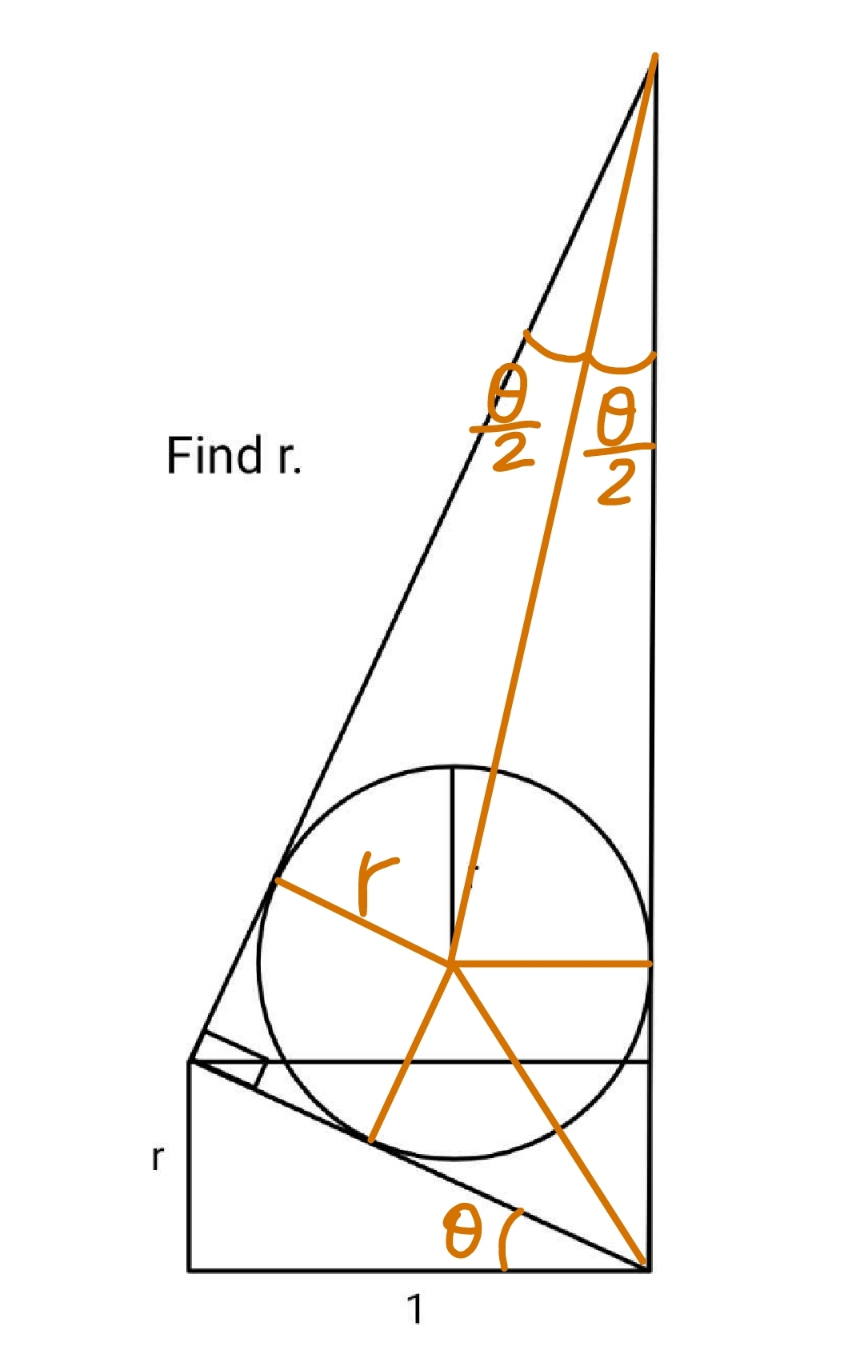
$$\mathrm{tan}\:\theta=\frac{{r}}{\mathrm{1}}={r} \\ $$$$\mathrm{cos}\:\theta=\frac{{r}+\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}}{\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\sqrt{\mathrm{1}+{r}^{\mathrm{2}} }−{r}} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}}{\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\theta}}−\mathrm{1}} \\ $$$${let}\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }=\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}+{t}\sqrt{\mathrm{1}+\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{2}{t}}\right)^{\mathrm{2}} }} \\ $$$${t}^{\mathrm{3}} −{t}^{\mathrm{2}} +\mathrm{5}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\left({s}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} −\left({s}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{5}\left({s}+\frac{\mathrm{1}}{\mathrm{3}}\right)−\mathrm{1}=\mathrm{0} \\ $$$${s}^{\mathrm{3}} +\frac{\mathrm{14}{s}}{\mathrm{3}}+\frac{\mathrm{16}}{\mathrm{27}}=\mathrm{0} \\ $$$${s}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}\sqrt{\mathrm{78}}}{\mathrm{9}}−\frac{\mathrm{8}}{\mathrm{27}}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}\sqrt{\mathrm{78}}}{\mathrm{9}}+\frac{\mathrm{8}}{\mathrm{27}}} \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{6}\sqrt{\mathrm{78}}−\mathrm{8}}−\sqrt[{\mathrm{3}}]{\mathrm{6}\sqrt{\mathrm{78}}+\mathrm{8}}\right) \\ $$$$\:\:\approx\mathrm{0}.\mathrm{206783} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\approx\mathrm{0}.\mathrm{432} \\ $$
Commented by ajfour last updated on 30/Jan/23
$${Thank}\:{you}\:{Sir}.\:{All}\:{correct}! \\ $$
