Question Number 185972 by Michaelfaraday last updated on 30/Jan/23
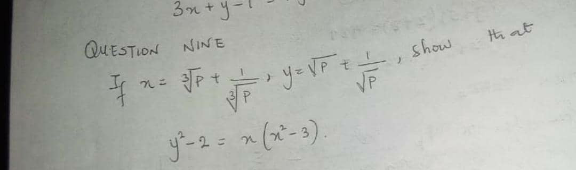
Answered by Rasheed.Sindhi last updated on 30/Jan/23
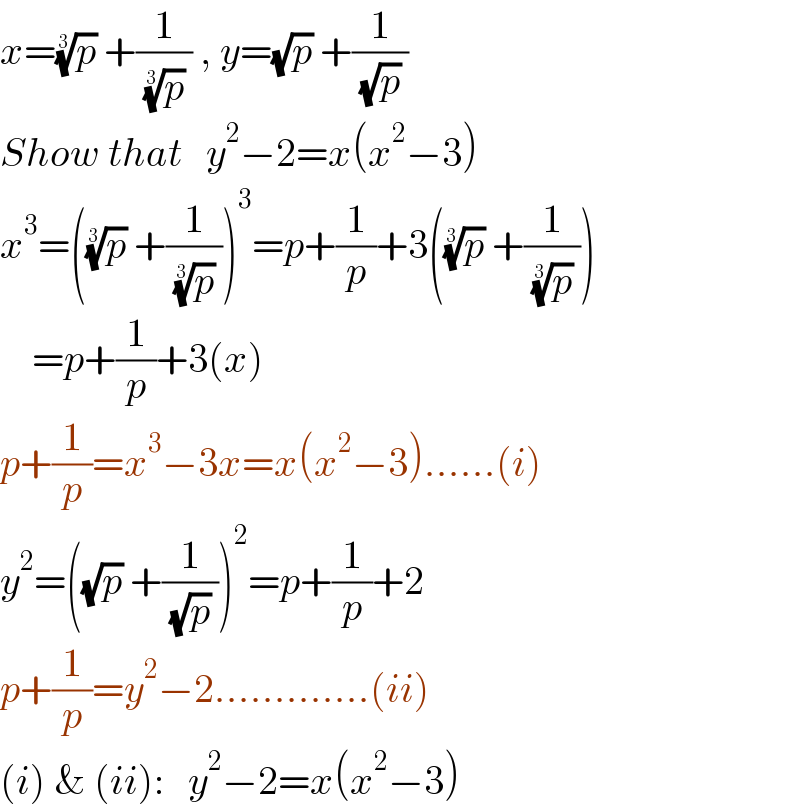
$${x}=\sqrt[{\mathrm{3}}]{{p}}\:+\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{p}}\:}\:,\:{y}=\sqrt{{p}}\:+\frac{\mathrm{1}}{\:\sqrt{{p}}\:} \\ $$$${Show}\:{that}\:\:\:{y}^{\mathrm{2}} −\mathrm{2}={x}\left({x}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$${x}^{\mathrm{3}} =\left(\sqrt[{\mathrm{3}}]{{p}}\:+\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{p}}\:}\right)^{\mathrm{3}} ={p}+\frac{\mathrm{1}}{{p}}+\mathrm{3}\left(\sqrt[{\mathrm{3}}]{{p}}\:+\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{p}}\:}\right) \\ $$$$\:\:\:\:={p}+\frac{\mathrm{1}}{{p}}+\mathrm{3}\left({x}\right) \\ $$$${p}+\frac{\mathrm{1}}{{p}}={x}^{\mathrm{3}} −\mathrm{3}{x}={x}\left({x}^{\mathrm{2}} −\mathrm{3}\right)……\left({i}\right) \\ $$$${y}^{\mathrm{2}} =\left(\sqrt{{p}}\:+\frac{\mathrm{1}}{\:\sqrt{{p}}\:}\right)^{\mathrm{2}} ={p}+\frac{\mathrm{1}}{{p}}+\mathrm{2} \\ $$$${p}+\frac{\mathrm{1}}{{p}}={y}^{\mathrm{2}} −\mathrm{2}………….\left({ii}\right) \\ $$$$\left({i}\right)\:\&\:\left({ii}\right):\:\:\:{y}^{\mathrm{2}} −\mathrm{2}={x}\left({x}^{\mathrm{2}} −\mathrm{3}\right) \\ $$
