Question Number 185978 by Rupesh123 last updated on 30/Jan/23
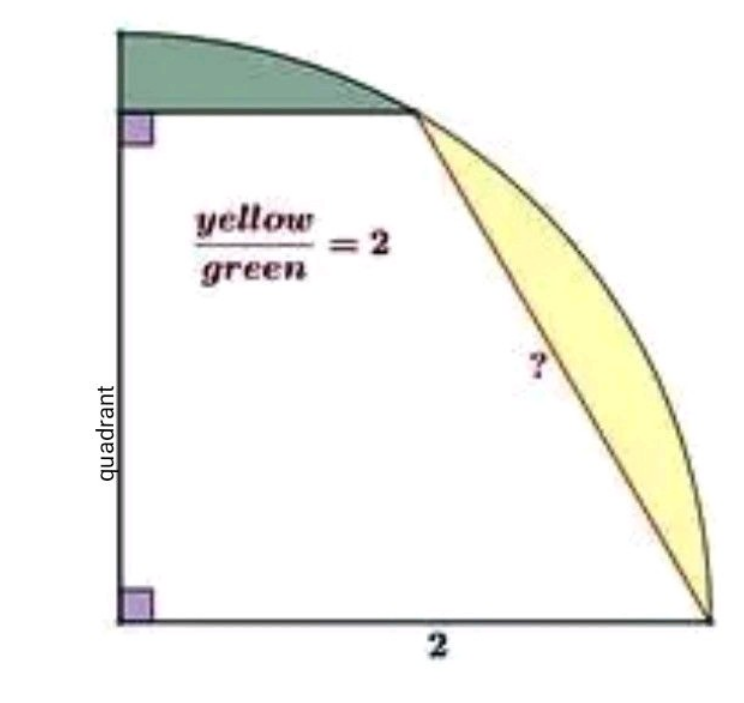
Answered by ajfour last updated on 30/Jan/23
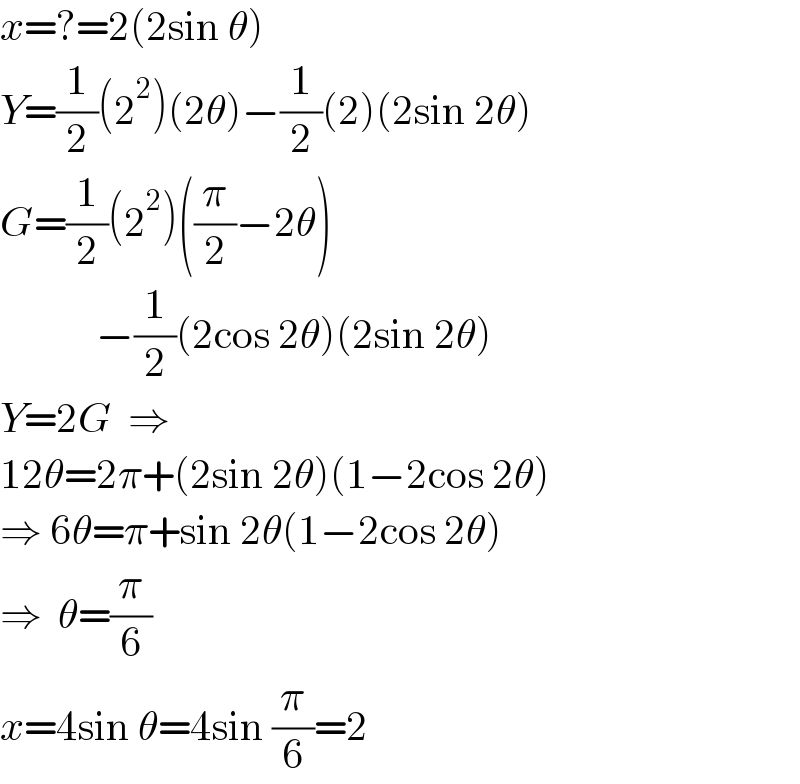
$${x}=?=\mathrm{2}\left(\mathrm{2sin}\:\theta\right) \\ $$$${Y}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}^{\mathrm{2}} \right)\left(\mathrm{2}\theta\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\right)\left(\mathrm{2sin}\:\mathrm{2}\theta\right) \\ $$$${G}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}^{\mathrm{2}} \right)\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2cos}\:\mathrm{2}\theta\right)\left(\mathrm{2sin}\:\mathrm{2}\theta\right) \\ $$$${Y}=\mathrm{2}{G}\:\:\Rightarrow \\ $$$$\mathrm{12}\theta=\mathrm{2}\pi+\left(\mathrm{2sin}\:\mathrm{2}\theta\right)\left(\mathrm{1}−\mathrm{2cos}\:\mathrm{2}\theta\right) \\ $$$$\Rightarrow\:\mathrm{6}\theta=\pi+\mathrm{sin}\:\mathrm{2}\theta\left(\mathrm{1}−\mathrm{2cos}\:\mathrm{2}\theta\right) \\ $$$$\Rightarrow\:\:\theta=\frac{\pi}{\mathrm{6}} \\ $$$${x}=\mathrm{4sin}\:\theta=\mathrm{4sin}\:\frac{\pi}{\mathrm{6}}=\mathrm{2} \\ $$
Answered by mr W last updated on 30/Jan/23

Commented by mr W last updated on 30/Jan/23

$$?=\mathrm{2} \\ $$
