Question Number 185982 by Shrinava last updated on 30/Jan/23
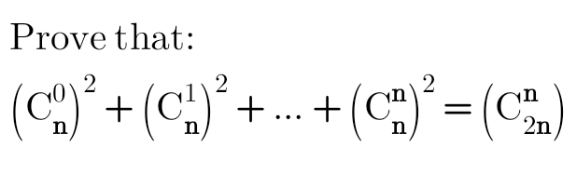
Answered by Mathspace last updated on 30/Jan/23
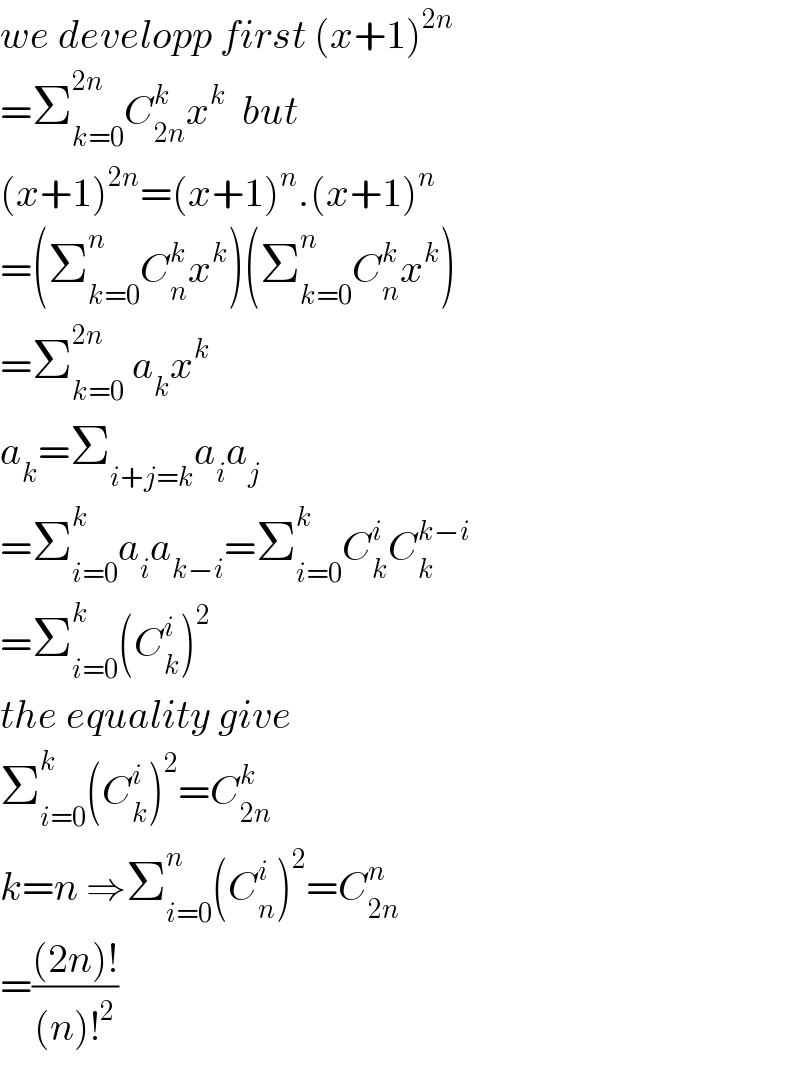
$${we}\:{developp}\:{first}\:\left({x}+\mathrm{1}\right)^{\mathrm{2}{n}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} {C}_{\mathrm{2}{n}} ^{{k}} {x}^{{k}} \:\:{but} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{2}{n}} =\left({x}+\mathrm{1}\right)^{{n}} .\left({x}+\mathrm{1}\right)^{{n}} \\ $$$$=\left(\sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} {x}^{{k}} \right)\left(\sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} {x}^{{k}} \right) \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \:{a}_{{k}} {x}^{{k}} \\ $$$${a}_{{k}} =\sum_{{i}+{j}={k}} {a}_{{i}} {a}_{{j}} \\ $$$$=\sum_{{i}=\mathrm{0}} ^{{k}} {a}_{{i}} {a}_{{k}−{i}} =\sum_{{i}=\mathrm{0}} ^{{k}} {C}_{{k}} ^{{i}} {C}_{{k}} ^{{k}−{i}} \\ $$$$=\sum_{{i}=\mathrm{0}} ^{{k}} \left({C}_{{k}} ^{{i}} \right)^{\mathrm{2}} \\ $$$${the}\:{equality}\:{give} \\ $$$$\sum_{{i}=\mathrm{0}} ^{{k}} \left({C}_{{k}} ^{{i}} \right)^{\mathrm{2}} ={C}_{\mathrm{2}{n}} ^{{k}} \\ $$$${k}={n}\:\Rightarrow\sum_{{i}=\mathrm{0}} ^{{n}} \left({C}_{{n}} ^{{i}} \right)^{\mathrm{2}} ={C}_{\mathrm{2}{n}} ^{{n}} \\ $$$$=\frac{\left(\mathrm{2}{n}\right)!}{\left({n}\right)!^{\mathrm{2}} } \\ $$
Commented by Shrinava last updated on 30/Jan/23
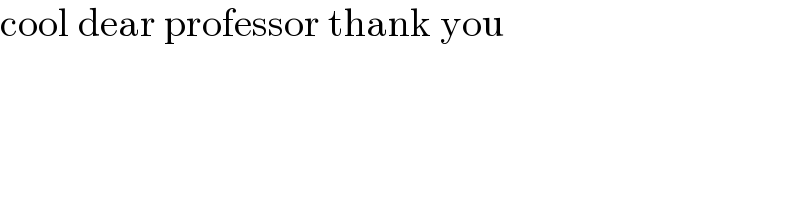
$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
