Question-185993

Question Number 185993 by ajfour last updated on 30/Jan/23

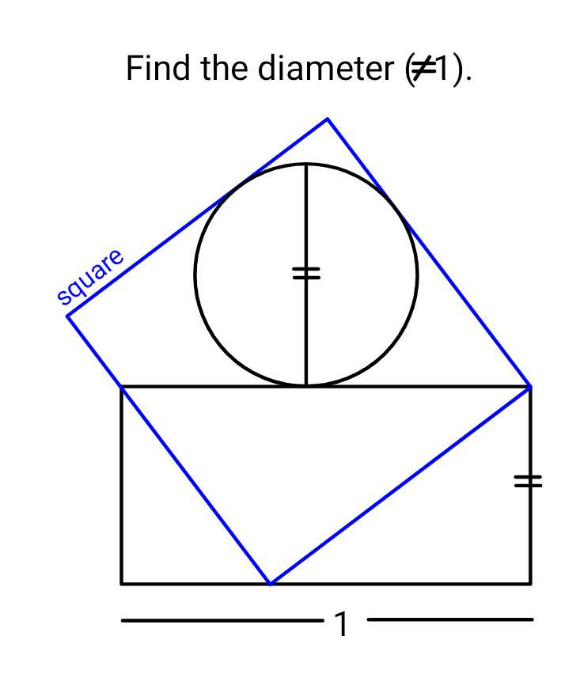
Answered by mr W last updated on 30/Jan/23

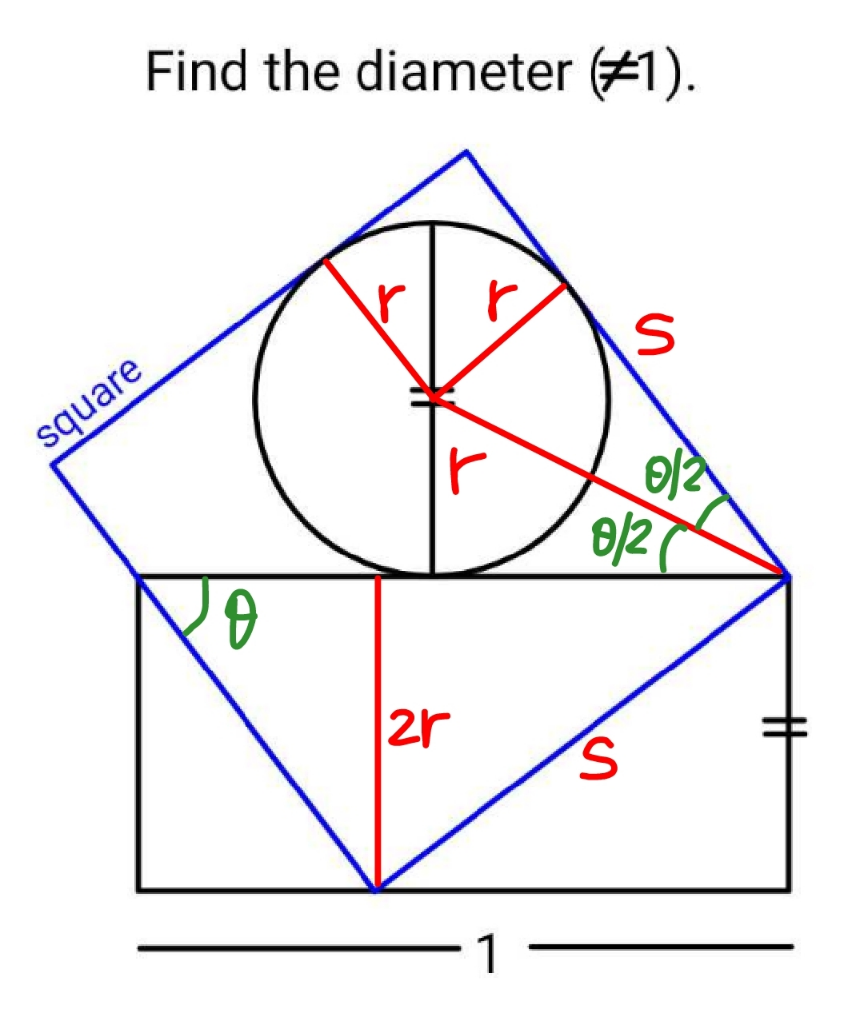
Commented by mr W last updated on 30/Jan/23

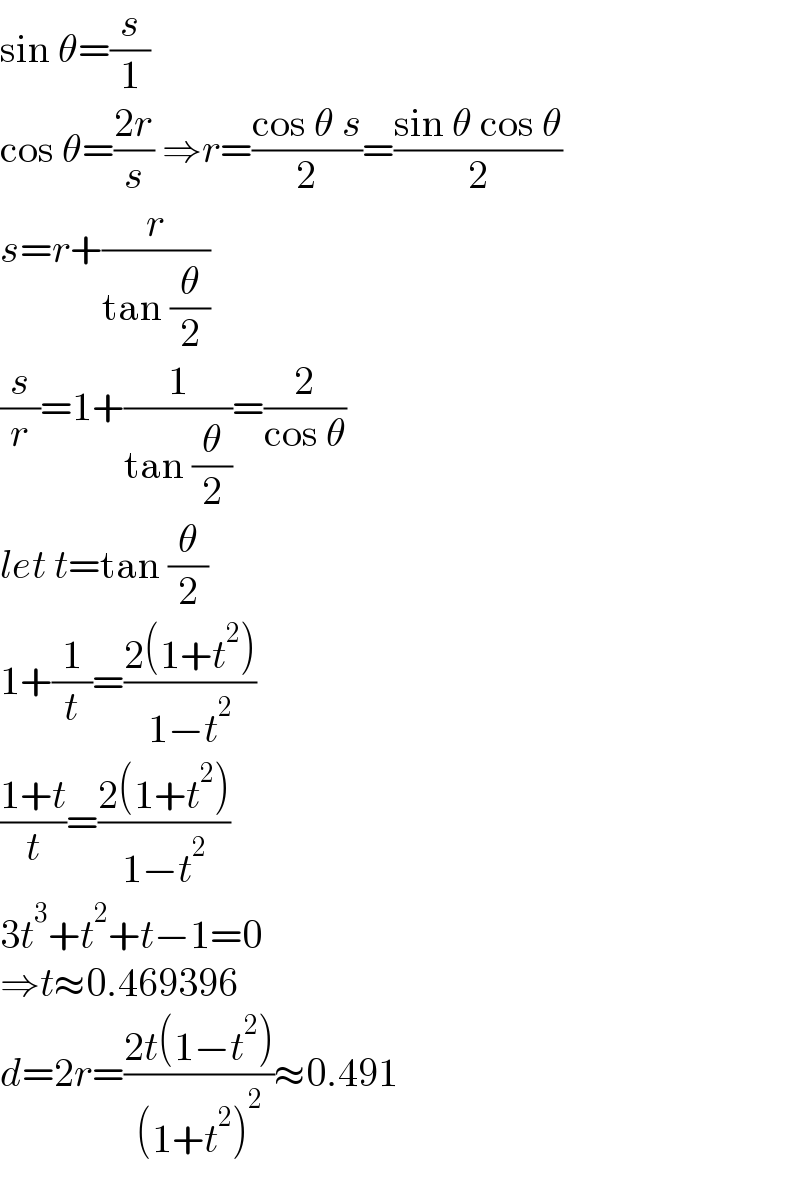
sin θ=(s/1) cos θ=((2r)/s) ⇒r=((cos θ s)/2)=((sin θ cos θ)/2) s=r+(r/(tan (θ/2))) (s/r)=1+(1/(tan (θ/2)))=(2/(cos θ)) let t=tan (θ/2) 1+(1/t)=((2(1+t^2 ))/(1−t^2 )) ((1+t)/t)=((2(1+t^2 ))/(1−t^2 )) 3t^3 +t^2 +t−1=0 ⇒t≈0.469396 d=2r=((2t(1−t^2 ))/((1+t^2 )^2 ))≈0.491

$$\mathrm{sin}\:\theta=\frac{{s}}{\mathrm{1}} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{2}{r}}{{s}}\:\Rightarrow{r}=\frac{\mathrm{cos}\:\theta\:{s}}{\mathrm{2}}=\frac{\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$${s}={r}+\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\frac{{s}}{{r}}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}=\frac{\mathrm{2}}{\mathrm{cos}\:\theta} \\ $$$${let}\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{{t}}=\frac{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}+{t}}{{t}}=\frac{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\mathrm{3}{t}^{\mathrm{3}} +{t}^{\mathrm{2}} +{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}\approx\mathrm{0}.\mathrm{469396} \\ $$$${d}=\mathrm{2}{r}=\frac{\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\approx\mathrm{0}.\mathrm{491} \\ $$

Commented by ajfour last updated on 31/Jan/23

$${yes}\:{sir},\:{thats}\:{right}! \\ $$$$\:{v}\:{nicely}\:\:{presented}. \\ $$

Facebook Tweet Pin

Question-185993

Leave a Reply Cancel reply