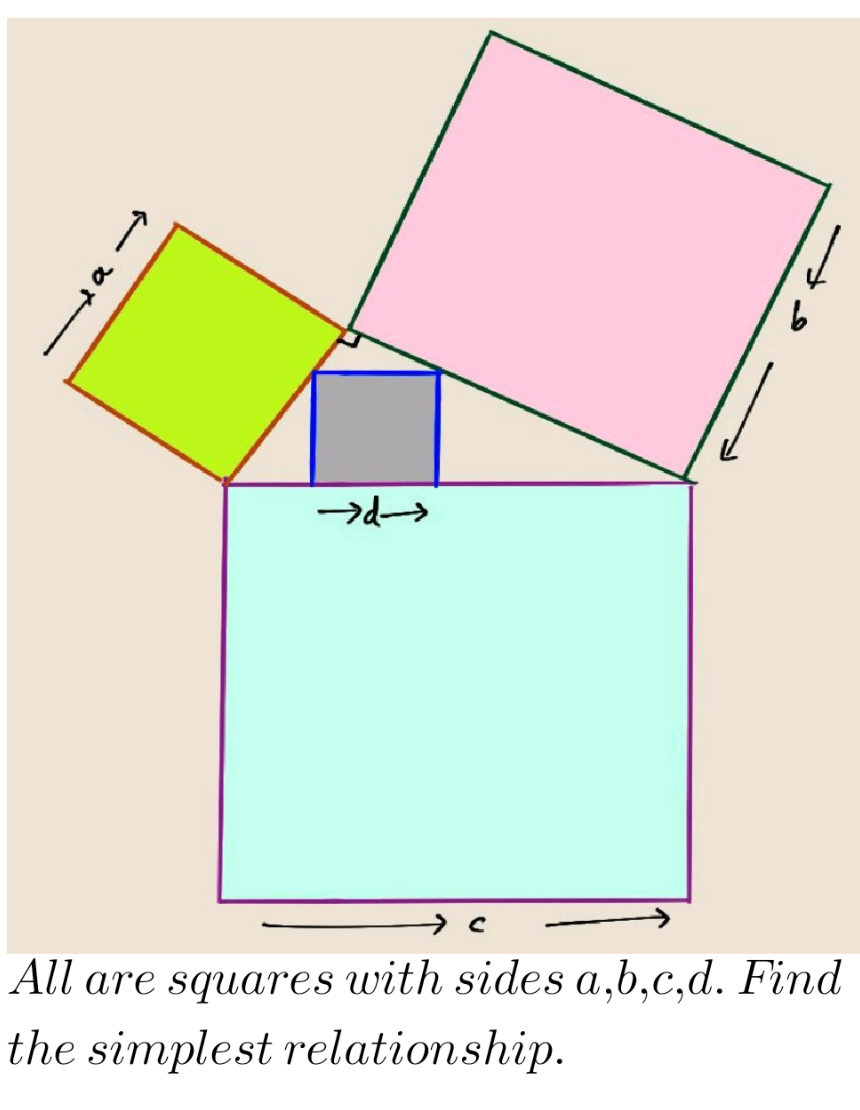
Question Number 186030 by Rupesh123 last updated on 31/Jan/23
Answered by ajfour last updated on 31/Jan/23

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={d}^{\mathrm{2}} \\ $$$$\left({a}−{x}\right){y}={d}^{\mathrm{2}} \\ $$$$\left({b}−{y}\right){x}={d}^{\mathrm{2}} \\ $$$${d}\left(\frac{{x}}{{y}}+\mathrm{1}+\frac{{y}}{{x}}\right)={c} \\ $$$$\Rightarrow\:{ay}={bx} \\ $$$$\Rightarrow\:\:\frac{{a}}{{b}}+\mathrm{1}+\frac{{b}}{{a}}=\frac{{c}}{{d}} \\ $$
Answered by mr W last updated on 31/Jan/23

$${generally}\:{for}\:{any}\:{triangle}: \\ $$$$\frac{{ch}}{\mathrm{2}}=\Delta=\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{\mathrm{4}} \\ $$$${h}=\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{\mathrm{2}{c}} \\ $$$$\frac{{h}−{d}}{{h}}=\frac{{d}}{{c}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{d}}=\frac{\mathrm{1}}{{c}}+\frac{\mathrm{1}}{{h}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{d}}=\frac{\mathrm{1}}{{c}}+\frac{\mathrm{2}{c}}{\:\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}} \\ $$$$ \\ $$$${in}\:{case}\:{of}\:{right}\:{angled}\:{triangle}: \\ $$$${h}=\frac{{ab}}{{c}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{d}}=\frac{\mathrm{1}}{{c}}+\frac{{c}}{{ab}} \\ $$
