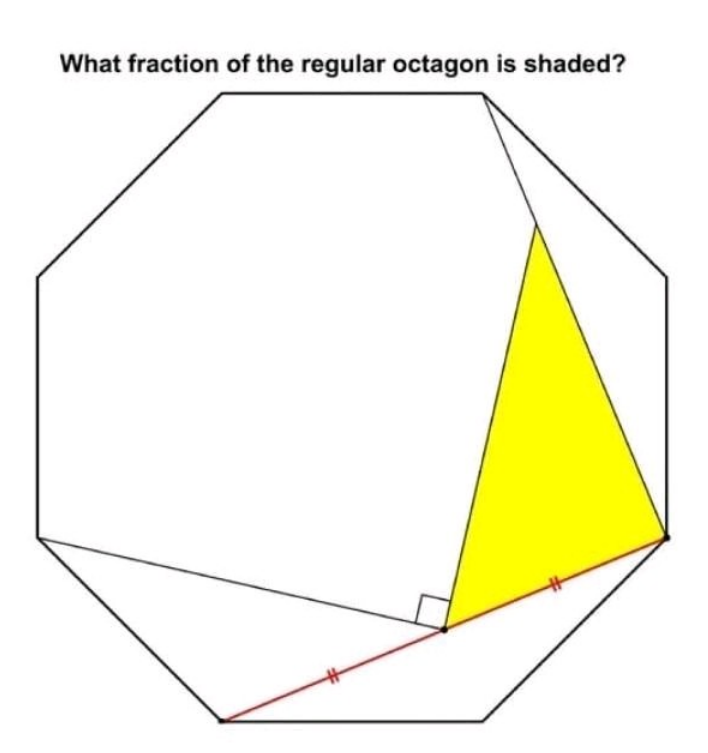
Question Number 186052 by Rupesh123 last updated on 31/Jan/23
Answered by HeferH last updated on 31/Jan/23
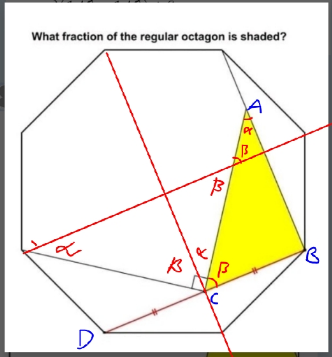
Commented by HeferH last updated on 31/Jan/23
![S : area of regular octagon S_1 :area shaded r: inradius S = 4[(((r−(r/( (√2))))r(√2))/2)] + (r(√2))^2 = ((r^2 (3+(√2)))/2) special triangle ABC (sides: k, k(√2), k(√3))⇒ BC = DC = (r/( (√2))) ⇒ AB = r ⇒ S_1 = (r^2 /(2(√2))) (S_1 /S) = (r^2 /(2(√2))) ∙ (2/(r^2 (3 + (√2)))) = (1/(3(√2)+2)) = ((3(√2)−2)/(14))](https://www.tinkutara.com/question/Q186068.png)
$${S}\::\:{area}\:{of}\:{regular}\:{octagon} \\ $$$${S}_{\mathrm{1}} :{area}\:{shaded} \\ $$$$\:{r}:\:{inradius} \\ $$$$\:{S}\:=\:\mathrm{4}\left[\frac{\left({r}−\frac{{r}}{\:\sqrt{\mathrm{2}}}\right){r}\sqrt{\mathrm{2}}}{\mathrm{2}}\right]\:+\:\left({r}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:=\:\frac{{r}^{\mathrm{2}} \left(\mathrm{3}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$\:{special}\:{triangle}\:{ABC}\:\left({sides}:\:{k},\:{k}\sqrt{\mathrm{2}},\:{k}\sqrt{\mathrm{3}}\right)\Rightarrow \\ $$$$\:{BC}\:=\:{DC}\:=\:\frac{{r}}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\:{AB}\:=\:{r} \\ $$$$\:\:\Rightarrow\:{S}_{\mathrm{1}} \:=\:\frac{{r}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}}\: \\ $$$$\:\frac{{S}_{\mathrm{1}} }{{S}}\:=\:\frac{{r}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}}\:\centerdot\:\frac{\mathrm{2}}{{r}^{\mathrm{2}} \left(\mathrm{3}\:+\:\sqrt{\mathrm{2}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{14}} \\ $$
