Question Number 186125 by Mingma last updated on 01/Feb/23

Answered by som(math1967) last updated on 01/Feb/23
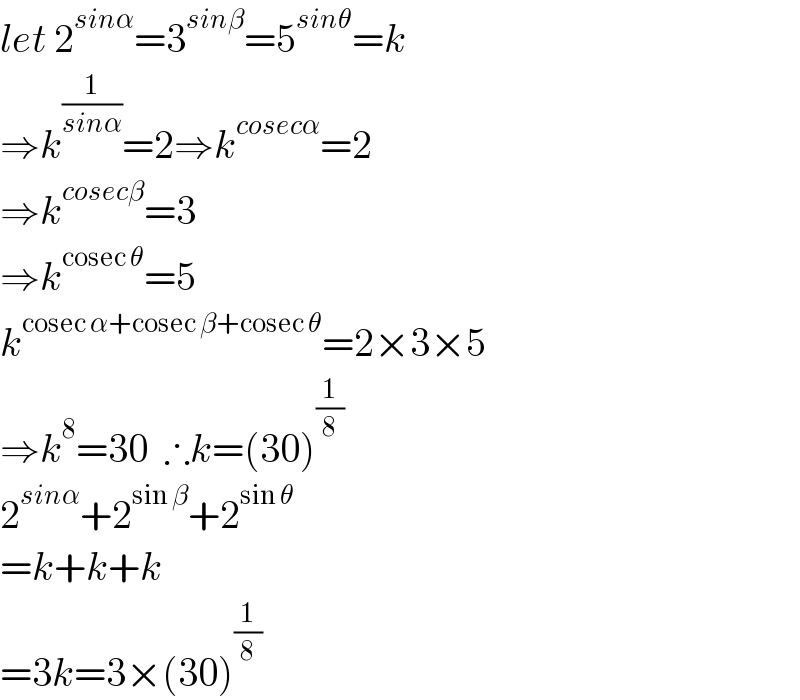
$${let}\:\mathrm{2}^{{sin}\alpha} =\mathrm{3}^{{sin}\beta} =\mathrm{5}^{{sin}\theta} ={k} \\ $$$$\Rightarrow{k}^{\frac{\mathrm{1}}{{sin}\alpha}} =\mathrm{2}\Rightarrow{k}^{{cosec}\alpha} =\mathrm{2} \\ $$$$\Rightarrow{k}^{{cosec}\beta} =\mathrm{3} \\ $$$$\Rightarrow{k}^{\mathrm{cosec}\:\theta} =\mathrm{5} \\ $$$${k}^{\mathrm{cosec}\:\alpha+\mathrm{cosec}\:\beta+\mathrm{cosec}\:\theta} =\mathrm{2}×\mathrm{3}×\mathrm{5} \\ $$$$\Rightarrow{k}^{\mathrm{8}} =\mathrm{30}\:\:\therefore{k}=\left(\mathrm{30}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} \\ $$$$\mathrm{2}^{{sin}\alpha} +\mathrm{2}^{\mathrm{sin}\:\beta} +\mathrm{2}^{\mathrm{sin}\:\theta} \\ $$$$={k}+{k}+{k} \\ $$$$=\mathrm{3}{k}=\mathrm{3}×\left(\mathrm{30}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} \\ $$
