Question Number 186144 by Rupesh123 last updated on 01/Feb/23

Commented by mr W last updated on 01/Feb/23
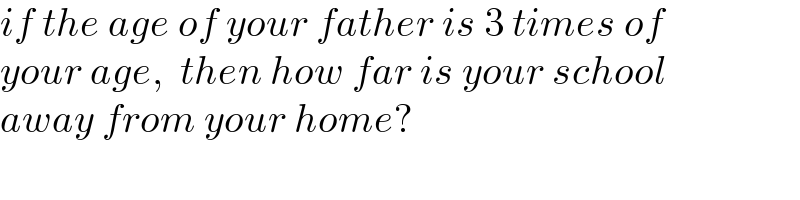
$${if}\:{the}\:{age}\:{of}\:{your}\:{father}\:{is}\:\mathrm{3}\:{times}\:{of} \\ $$$${your}\:{age},\:\:{then}\:{how}\:{far}\:{is}\:{your}\:{school}\: \\ $$$${away}\:{from}\:{your}\:{home}? \\ $$
Commented by Frix last updated on 01/Feb/23

$$\frac{\mathrm{cos}\:\mathrm{3}{x}}{\mathrm{cos}\:{x}}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 01/Feb/23

$$\frac{\mathrm{cos}\:\mathrm{3}{x}}{\mathrm{cos}\:{x}}=\frac{\mathrm{1}}{\mathrm{3}}\:{is}\:{an}\:{equation}\:{which}\: \\ $$$${delivers}\:{values}\:{for}\:{x}. \\ $$$${in}\:\int_{{A}} ^{{B}} \frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}{dx}\:{the}\:\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}\:{is}\:{a}\:{function} \\ $$$${of}\:{x}\:{which}\:{is}\:{integrated}\:{for}\:{x}\:{from}\: \\ $$$${A}\:{to}\:{B}. \\ $$$$\int_{{A}} ^{{B}} \frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}{dx}\:{can}\:{also}\:{be}\:{written}\:{as} \\ $$$$\int_{{A}} ^{{B}} \frac{\mathrm{sin}\:\mathrm{3}{t}}{\mathrm{sin}\:{t}}{dt}\:{or}\:\int_{{A}} ^{{B}} \frac{\mathrm{sin}\:\mathrm{3}{u}}{\mathrm{sin}\:{u}}{du}\:{etc}.,\:{it} \\ $$$${delivers}\:{a}\:{value}\:{which}\:{only}\:{depends}\:{on} \\ $$$${A}\:{and}\:{B},\:{no}\:{matter}\:{if}\:{you}\:{write} \\ $$$$\int_{{A}} ^{{B}} \frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}{dx}\:{or}\:\int_{{A}} ^{{B}} \frac{\mathrm{sin}\:\mathrm{3}{t}}{\mathrm{sin}\:{t}}{dt}\:{or}\:\int_{{A}} ^{{B}} \frac{\mathrm{sin}\:\mathrm{3}{u}}{\mathrm{sin}\:{u}}{du}. \\ $$$${the}\:{solution}\:{of}\:{the}\:{first}\:{equation}\: \\ $$$${has}\:{nothing}\:{to}\:{do}\:{with}\:{the}\:{integral}! \\ $$
Commented by Frix last updated on 01/Feb/23
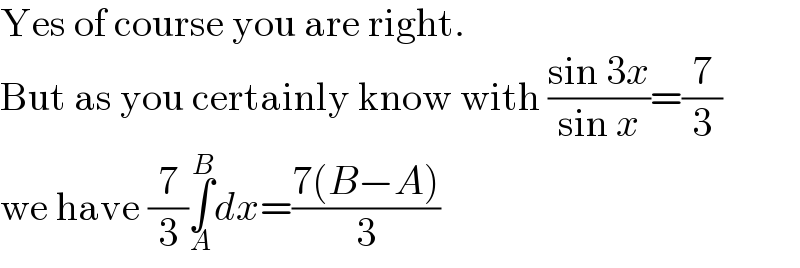
$$\mathrm{Yes}\:\mathrm{of}\:\mathrm{course}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}. \\ $$$$\mathrm{But}\:\mathrm{as}\:\mathrm{you}\:\mathrm{certainly}\:\mathrm{know}\:\mathrm{with}\:\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{7}}{\mathrm{3}}\underset{{A}} {\overset{{B}} {\int}}{dx}=\frac{\mathrm{7}\left({B}−{A}\right)}{\mathrm{3}} \\ $$
Commented by Frix last updated on 01/Feb/23
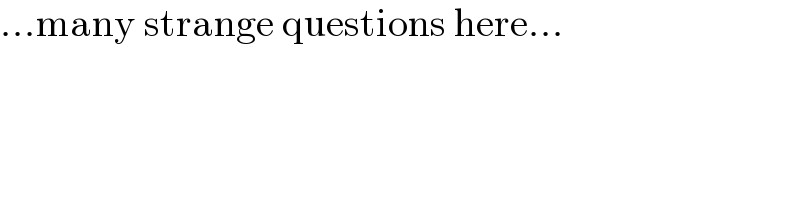
$$…\mathrm{many}\:\mathrm{strange}\:\mathrm{questions}\:\mathrm{here}… \\ $$
Commented by mr W last updated on 01/Feb/23
![no, i don′t agree with you. when ∫_A ^B ((sin 3x)/(sin x))dx is written, it means x is a variable in the range [A,B]. there is no reason to say ((sin 3x)/(sin x))=constant=(7/3). you could be right, when it is ∫_A ^B ((sin 3x)/(sin x)) dt.](https://www.tinkutara.com/question/Q186166.png)
$${no},\:{i}\:{don}'{t}\:{agree}\:{with}\:{you}. \\ $$$${when}\:\int_{{A}} ^{{B}} \frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}{dx}\:{is}\:{written},\:{it}\:{means} \\ $$$${x}\:{is}\:{a}\:{variable}\:{in}\:{the}\:{range}\:\left[{A},{B}\right].\: \\ $$$${there}\:{is}\:{no}\:{reason}\:{to}\:{say}\: \\ $$$$\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}={constant}=\frac{\mathrm{7}}{\mathrm{3}}. \\ $$$${you}\:{could}\:{be}\:{right},\:{when}\:{it}\:{is} \\ $$$$\int_{{A}} ^{{B}} \frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}\:{dt}. \\ $$
Commented by ajfour last updated on 01/Feb/23
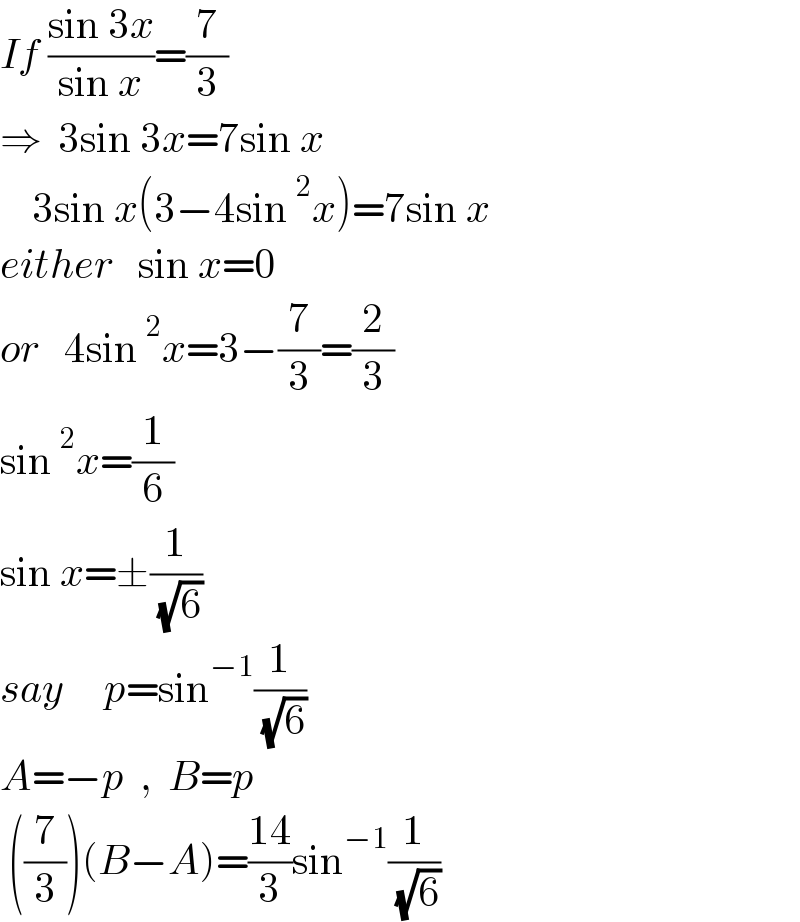
$${If}\:\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}=\frac{\mathrm{7}}{\mathrm{3}} \\ $$$$\Rightarrow\:\:\mathrm{3sin}\:\mathrm{3}{x}=\mathrm{7sin}\:{x} \\ $$$$\:\:\:\:\mathrm{3sin}\:{x}\left(\mathrm{3}−\mathrm{4sin}\:^{\mathrm{2}} {x}\right)=\mathrm{7sin}\:{x} \\ $$$${either}\:\:\:\mathrm{sin}\:{x}=\mathrm{0} \\ $$$${or}\:\:\:\mathrm{4sin}\:^{\mathrm{2}} {x}=\mathrm{3}−\frac{\mathrm{7}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} {x}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{sin}\:{x}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}} \\ $$$${say}\:\:\:\:\:{p}=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}} \\ $$$${A}=−{p}\:\:,\:\:{B}={p} \\ $$$$\:\left(\frac{\mathrm{7}}{\mathrm{3}}\right)\left({B}−{A}\right)=\frac{\mathrm{14}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}} \\ $$
Commented by prakash jain last updated on 02/Feb/23
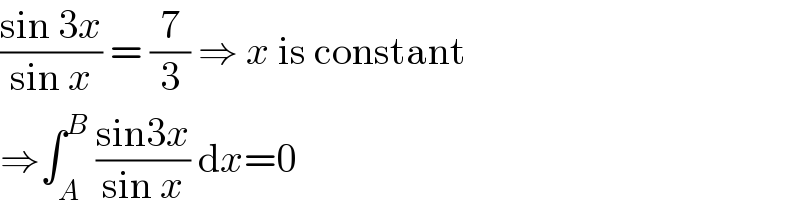
$$\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{7}}{\mathrm{3}}\:\Rightarrow\:{x}\:\mathrm{is}\:\mathrm{constant} \\ $$$$\Rightarrow\int_{{A}} ^{{B}} \:\frac{\mathrm{sin3}{x}}{\mathrm{sin}\:{x}}\:\mathrm{d}{x}=\mathrm{0} \\ $$
Commented by ajfour last updated on 02/Feb/23

$${hi} \\ $$
