Question Number 186230 by Noorzai last updated on 02/Feb/23

Answered by Rasheed.Sindhi last updated on 02/Feb/23
![(10K+K)(10L+L)= L178 ^(−) 11K∙11L= L178 ^(−) L178 ^(−) is divisible by 11 ∴ (L+7)−(1+8)=0,11,... L−2=0,11,... L=2^(✓) ,13^(×) ,... [∵ 0≤L≤9] 11K×22=2178 K=2178/(22×11)=9 K+L=9+2=11](https://www.tinkutara.com/question/Q186239.png)
$$\left(\mathrm{10K}+\mathrm{K}\right)\left(\mathrm{10L}+\mathrm{L}\right)=\overline {\:\mathrm{L178}\:} \\ $$$$\mathrm{11K}\centerdot\mathrm{11L}=\overline {\:\mathrm{L178}\:} \\ $$$$\overline {\:\mathrm{L178}\:}\:{is}\:{divisible}\:{by}\:\mathrm{11} \\ $$$$\therefore\:\left(\mathrm{L}+\mathrm{7}\right)−\left(\mathrm{1}+\mathrm{8}\right)=\mathrm{0},\mathrm{11},… \\ $$$$\mathrm{L}−\mathrm{2}=\mathrm{0},\mathrm{11},… \\ $$$$\mathrm{L}=\overset{\checkmark} {\mathrm{2}},\overset{×} {\mathrm{13}},…\:\:\left[\because\:\:\mathrm{0}\leqslant\mathrm{L}\leqslant\mathrm{9}\right] \\ $$$$\mathrm{11K}×\mathrm{22}=\mathrm{2178} \\ $$$$\mathrm{K}=\mathrm{2178}/\left(\mathrm{22}×\mathrm{11}\right)=\mathrm{9} \\ $$$$\mathrm{K}+\mathrm{L}=\mathrm{9}+\mathrm{2}=\mathrm{11} \\ $$
Answered by mr W last updated on 02/Feb/23
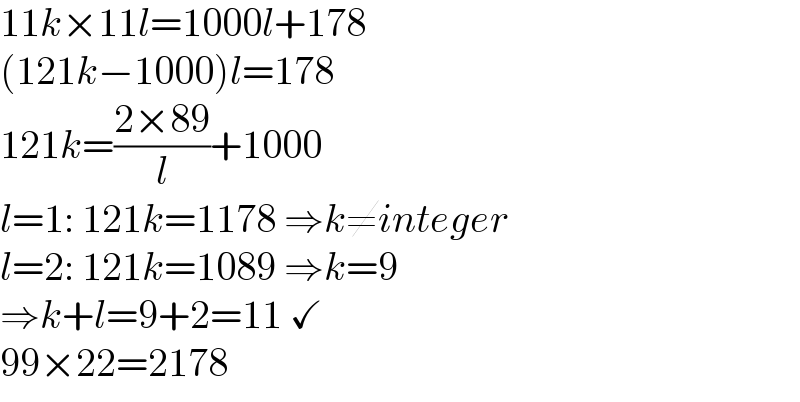
$$\mathrm{11}{k}×\mathrm{11}{l}=\mathrm{1000}{l}+\mathrm{178} \\ $$$$\left(\mathrm{121}{k}−\mathrm{1000}\right){l}=\mathrm{178} \\ $$$$\mathrm{121}{k}=\frac{\mathrm{2}×\mathrm{89}}{{l}}+\mathrm{1000} \\ $$$${l}=\mathrm{1}:\:\mathrm{121}{k}=\mathrm{1178}\:\Rightarrow{k}\neq{integer} \\ $$$${l}=\mathrm{2}:\:\mathrm{121}{k}=\mathrm{1089}\:\Rightarrow{k}=\mathrm{9} \\ $$$$\Rightarrow{k}+{l}=\mathrm{9}+\mathrm{2}=\mathrm{11}\:\checkmark \\ $$$$\mathrm{99}×\mathrm{22}=\mathrm{2178} \\ $$
