Question Number 186253 by ajfour last updated on 02/Feb/23
Commented by ajfour last updated on 02/Feb/23

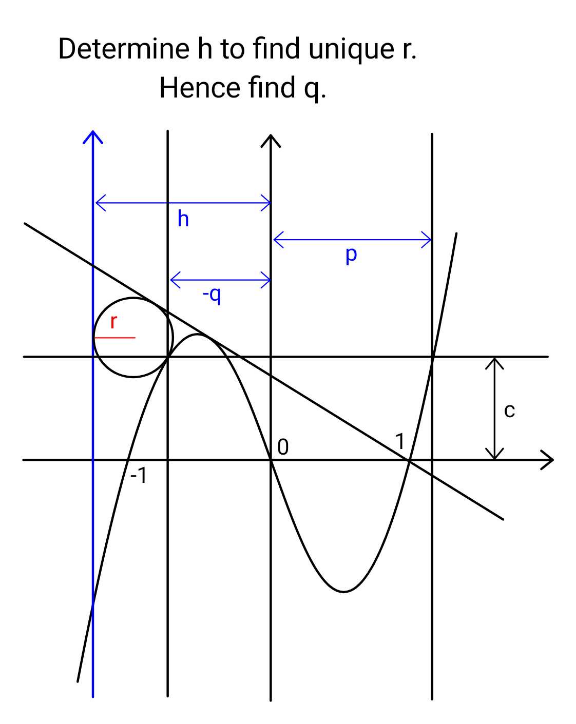
$${The}\:{curve}\:{is}\:{a}\:\:{cubic}\:\left(\:{y}={x}^{\mathrm{3}} −{x}\right), \\ $$$$\:{and}\:{that}\:\:\mathrm{0}<{c}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\:\centerdot \\ $$$${Let}\:{circle}\:{not}\:{necessarily}\:{be}\: \\ $$$${tangent}\:{to}\:{cubic}\:{curve}\:{at}\:\left({q},\:{c}\right). \\ $$
Answered by a.lgnaoui last updated on 04/Feb/23
![equation de droite (D) y=ax+b x=1 y=0 Extremums=(−((√3)/3),+((√3)/3)) conciderons B(−((√3)/3),((2(√3))/9))∈(D) y=((1−(√3))/3)x+(((√3) −1)/3) cercle (C)coupe la ciurbe enC C(−q,q−q^3 ) ,tangente enC est (dy/dx)(x=−q)=3q^2 −1=tan θ r+rcos θ=h−(−q)=h+q r=((h+q)/(1+(1/( (√(1+tan^2 θ))))))=(((h+q)(√(1+tan^2 θ )))/(1+(√(1+tan^2 θ)))) r=(((h+q)(√((q^2 −(1/3))^2 +(1/9))))/( (√((q^2 −(1/3))^2 +(1/9))) +(1/3))) la droite(D)tangente au cercle (C) en C tan ψ=((1−(√3))/3) (x−x_0 )^2 +(y−y_0 )^2 =r^2 y=(√(r^2 −(x−x_0 )^2 )) +y_0 (dy/dx)=((−2(x−x_0 ))/(2(√(r^2 −(x−x_0 )^2 )) +y_0 ))=((1−(√3))/3) (1) x−x_0 =z −6z=(((1−(√3))/3))(y_0 +2(√(r^2 −z^2 )) ) (√(r^2 −z^2 )) =((−9z)/(1−(√3)))−(y_0 /2) r^2 −z^2 =((81z^2 )/((1−(√3) )^2 ))−((9y_0 )/((85−2(√3) )(1−(√3) )))z+(y_0 ^2 /4) [((85−2(√3))/((1−(√(3)^2 ))))]z^2 −((9y_0 )/((1−(√(3)))(85−2(√(3)))))z+(y_0 ^2 /4)−r^2 =0 △=((81y_0 ^2 )/((1−(√3) )^2 (85−2(√3) )^2 ))−((y_0 ^2 −4r^2 )/((1−(√3) )^2 ))(85−2(√3) ) =81y_0 ^2 −(y_0 ^2 −4r^2 )(85−2(√3) )^3 =0 [81−(85−2(√3) )^3 ]y_0^ ^2 = 4r^2 (85−2(√3) )^3 y_0 =((2r(√((85−2(√3) )^3 )))/((85−2(√3) )^3 −81)) z=((9−9(√3))/(2(85−2(√3) )^2 ))y_0 en remplacant dans z en deduire x−x_0 dans l equation de cerxle y=y_0 +(√(r^2 −z^2 )) (1)⇒((1−(√3))/3)=((2r(√((85−2(√3) )^3 )))/((85−2(√3) )^3 −81))+ r(√(1−((81(1−(√3) )^2 )/(2(85−2(√3) )[(85−2(√3) )^3 −81])))) (A suivre)................ after calcul ((1−(√3))/3)≅r=(((h+q)(√((q^2 −(1/3))^2 +(1/9))))/( (√((q^2 −(1/3))^2 +(1/9))) +(1/3))) (h+q)(√((q^2 −(1/3))+(1/9)))=(((1−(√3))/3))[(√((q^2 −(1/3))^2 +(1/9))) +(1/3)] h+q=(((1−(√3))/3))(((√((q^2 −(1/3))^2 +(1/9))) +(1/3))/( (√((q^2 −(1/3))^2 +(1/9))))) h=(((1−(√3))/3))(((√((q^2 −(1/3))^2 +(1/9))) +(1/3))/( (√((q^2 −(1/3))^2 +(1/9)))))−q h=((1−(√3))/3)(1+(1/(3×(√((q^2 −(1/3))^2 +(1/9))))))−q h=((1−(√3))/3)+((1−(√3))/( (√((9q^2 −3)^2 +9)) ))−q ∣h+q∣=(((√3) −1)/3)+(((√3) −1)/( (√((9q^2 −3)^2 +9)) )) h+q=r+(r/( (√(1+tanθ^2 ))))=r(1+(1/( (√(1+(((1−(√3))/3))^2 ))))) h+q=r+((3r)/( (√(13−2(√3))))) (((√3) −1)/( (√(13−2(√3)))))=(((√3) −1)/( (√((9q^2 −3)^2 +9)))) (9q^2 −3)^2 =4−2(√3) q^2 =(((√(4−2(√3) )) +3)/9) q=((√((√(4−2(√3) )) +3))/3)=1,244 donc ∣h∣=1,18 r=(((√3) −1)/3)=0,244](https://www.tinkutara.com/question/Q186377.png)
$${equation}\:{de}\:{droite}\:\left({D}\right) \\ $$$${y}={ax}+{b}\:\:\:{x}=\mathrm{1}\:\:{y}=\mathrm{0} \\ $$$${Extremums}=\left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}},+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right) \\ $$$${conciderons}\:\:\:{B}\left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}},\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\right)\in\left({D}\right) \\ $$$${y}=\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}{x}+\frac{\sqrt{\mathrm{3}}\:−\mathrm{1}}{\mathrm{3}} \\ $$$${cercle}\:\left({C}\right){coupe}\:{la}\:{ciurbe}\:{en}\mathrm{C} \\ $$$$\mathrm{C}\left(−{q},{q}−{q}^{\mathrm{3}} \right)\:\:\:,{tangente}\:{en}\mathrm{C}\:\mathrm{est} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\left(\mathrm{x}=−\mathrm{q}\right)=\mathrm{3q}^{\mathrm{2}} −\mathrm{1}=\mathrm{tan}\:\theta \\ $$$${r}+{r}\mathrm{cos}\:\theta={h}−\left(−{q}\right)={h}+{q} \\ $$$${r}=\frac{{h}+{q}}{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}}}=\frac{\left({h}+{q}\right)\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\:}}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}} \\ $$$${r}=\frac{\left({h}+{q}\right)\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}}{\:\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}\:+\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${la}\:{droite}\left({D}\right){tangente}\:{au}\:{cercle}\:\left({C}\right)\:{en}\:\mathrm{C} \\ $$$$\mathrm{tan}\:\psi=\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\left({x}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} +\left({y}−{y}_{\mathrm{0}} \right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${y}=\sqrt{{r}^{\mathrm{2}} −\left({x}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} \:}\:+{y}_{\mathrm{0}} \\ $$$$\frac{{dy}}{{dx}}=\frac{−\mathrm{2}\left({x}−{x}_{\mathrm{0}} \right)}{\mathrm{2}\sqrt{{r}^{\mathrm{2}} −\left({x}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} \:}\:+{y}_{\mathrm{0}} }=\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\:\left(\mathrm{1}\right) \\ $$$${x}−{x}_{\mathrm{0}} ={z}\:\:\: \\ $$$$−\mathrm{6}{z}=\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\left({y}_{\mathrm{0}} +\mathrm{2}\sqrt{{r}^{\mathrm{2}} −{z}^{\mathrm{2}} }\:\right) \\ $$$$\sqrt{{r}^{\mathrm{2}} −{z}^{\mathrm{2}} }\:=\frac{−\mathrm{9}{z}}{\mathrm{1}−\sqrt{\mathrm{3}}}−\frac{{y}_{\mathrm{0}} }{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −{z}^{\mathrm{2}} =\frac{\mathrm{81}{z}^{\mathrm{2}} }{\left(\mathrm{1}−\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} }−\frac{\mathrm{9}{y}_{\mathrm{0}} }{\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)\left(\mathrm{1}−\sqrt{\mathrm{3}}\:\right)}{z}+\frac{{y}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\left[\frac{\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}}{\left(\mathrm{1}−\sqrt{\left.\mathrm{3}\right)^{\mathrm{2}} }\right.}\right]{z}^{\mathrm{2}} −\frac{\mathrm{9}{y}_{\mathrm{0}} }{\left(\mathrm{1}−\sqrt{\left.\mathrm{3}\right)}\left(\mathrm{85}−\mathrm{2}\sqrt{\left.\mathrm{3}\right)}\right.\right.}{z}+\frac{{y}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{4}}−{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\bigtriangleup=\frac{\mathrm{81}{y}_{\mathrm{0}} ^{\mathrm{2}} }{\left(\mathrm{1}−\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} \left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} }−\frac{{y}_{\mathrm{0}} ^{\mathrm{2}} −\mathrm{4}{r}^{\mathrm{2}} }{\left(\mathrm{1}−\sqrt{\mathrm{3}}\:\:\right)^{\mathrm{2}} }\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\:\right) \\ $$$$ \\ $$$$=\mathrm{81}{y}_{\mathrm{0}} ^{\mathrm{2}} −\left({y}_{\mathrm{0}} ^{\mathrm{2}} −\mathrm{4}{r}^{\mathrm{2}} \right)\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$ \\ $$$$\left[\mathrm{81}−\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{3}} \right]{y}_{\mathrm{0}^{} } ^{\mathrm{2}} = \\ $$$$\mathrm{4}{r}^{\mathrm{2}} \left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{3}} \\ $$$$ \\ $$$${y}_{\mathrm{0}} =\frac{\mathrm{2}{r}\sqrt{\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\:\right)^{\mathrm{3}} \:}}{\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{3}} −\mathrm{81}}\: \\ $$$$ \\ $$$${z}=\frac{\mathrm{9}−\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{2}\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} }{y}_{\mathrm{0}} \\ $$$$ \\ $$$${en}\:{remplacant}\:{dans}\:{z} \\ $$$${en}\:{deduire}\:\:{x}−{x}_{\mathrm{0}} \\ $$$${dans}\:{l}\:{equation}\:{de}\:{cerxle} \\ $$$${y}={y}_{\mathrm{0}} +\sqrt{{r}^{\mathrm{2}} −{z}^{\mathrm{2}} \:\:} \\ $$$$\left(\mathrm{1}\right)\Rightarrow\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}=\frac{\mathrm{2}{r}\sqrt{\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{3}} }}{\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{3}} −\mathrm{81}}+ \\ $$$${r}\sqrt{\mathrm{1}−\frac{\mathrm{81}\left(\mathrm{1}−\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)\left[\left(\mathrm{85}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{3}} −\mathrm{81}\right]}} \\ $$$$ \\ $$$$\left({A}\:{suivre}\right)……………. \\ $$$${after}\:{calcul} \\ $$$$\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\cong{r}=\frac{\left({h}+{q}\right)\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}}{\:\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}\:+\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$ \\ $$$$\left({h}+{q}\right)\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{9}}}=\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\left[\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}\:+\frac{\mathrm{1}}{\mathrm{3}}\right] \\ $$$${h}+{q}=\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\frac{\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}\:+\frac{\mathrm{1}}{\mathrm{3}}}{\:\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}} \\ $$$$ \\ $$$${h}=\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\frac{\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}\:+\frac{\mathrm{1}}{\mathrm{3}}}{\:\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}}−{q} \\ $$$${h}=\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}×\sqrt{\left({q}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{9}}}}\right)−{q} \\ $$$$\boldsymbol{{h}}=\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\:\sqrt{\left(\mathrm{9}{q}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} +\mathrm{9}}\:}−{q} \\ $$$$ \\ $$$$\mid\boldsymbol{{h}}+\boldsymbol{{q}}\mid=\frac{\sqrt{\mathrm{3}}\:−\mathrm{1}}{\mathrm{3}}+\frac{\sqrt{\mathrm{3}}\:−\mathrm{1}}{\:\sqrt{\left(\mathrm{9}\boldsymbol{{q}}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} +\mathrm{9}}\:} \\ $$$${h}+{q}={r}+\frac{{r}}{\:\sqrt{\mathrm{1}+\mathrm{tan}\theta\:^{\mathrm{2}} }}={r}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{3}}\right)^{\mathrm{2}} }}\right) \\ $$$${h}+{q}={r}+\frac{\mathrm{3}{r}}{\:\sqrt{\mathrm{13}−\mathrm{2}\sqrt{\mathrm{3}}}} \\ $$$$\frac{\sqrt{\mathrm{3}}\:−\mathrm{1}}{\:\sqrt{\mathrm{13}−\mathrm{2}\sqrt{\mathrm{3}}}}=\frac{\sqrt{\mathrm{3}}\:−\mathrm{1}}{\:\sqrt{\left(\mathrm{9}{q}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} +\mathrm{9}}} \\ $$$$\left(\mathrm{9}{q}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} =\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${q}^{\mathrm{2}} =\frac{\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:}\:+\mathrm{3}}{\mathrm{9}} \\ $$$${q}=\frac{\sqrt{\sqrt{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:}\:\:+\mathrm{3}}}{\mathrm{3}}=\mathrm{1},\mathrm{244} \\ $$$${donc} \\ $$$$\mid{h}\mid=\mathrm{1},\mathrm{18} \\ $$$${r}=\frac{\sqrt{\mathrm{3}}\:−\mathrm{1}}{\mathrm{3}}=\mathrm{0},\mathrm{244} \\ $$$$ \\ $$
Commented by ajfour last updated on 04/Feb/23

$${Center}\:{of}\:{circle}\:{Q}. \\ $$$${Q}\left({q}−{r}\mathrm{sin}\:\theta,\:{c}+{r}\mathrm{cos}\:\theta\right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{3}{q}^{\mathrm{2}} −\mathrm{1} \\ $$$${Tangent}:\:\:\:\:{y}=−{m}\left({x}−\mathrm{1}\right) \\ $$$${m}\left(\mathrm{1}−{x}\right)={x}^{\mathrm{3}} −{x} \\ $$$${x}^{\mathrm{3}} +\left({m}−\mathrm{1}\right){x}−{m}=\mathrm{0} \\ $$$${double}\:{root}\:\Rightarrow\:\frac{{m}^{\mathrm{2}} }{\mathrm{4}}=\frac{\left(\mathrm{1}−{m}\right)^{\mathrm{3}} }{\mathrm{27}} \\ $$$${required}\:{m}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${Tangent}:\:\:\:\mathrm{4}{y}=\mathrm{1}−{x} \\ $$$${h}−{r}={q}−{r}\mathrm{sin}\:\theta \\ $$$$−\sqrt{\mathrm{17}}{r}=\mathrm{4}\left({c}+{r}\mathrm{cos}\:\theta\right)−\frac{\sqrt{\mathrm{1}+\mathrm{tan}\:\theta}}{\:\sqrt{\mathrm{3}}}−{r}\mathrm{sin}\:\theta−\mathrm{1} \\ $$$$\frac{\mathrm{tan}\:\theta+\mathrm{1}}{\mathrm{3}}=\left\{\mathrm{4}{c}−\mathrm{1}+{r}\left(\mathrm{4cos}\:\theta−\mathrm{sin}\:\theta+\sqrt{\mathrm{17}}\right)\right\}^{\mathrm{2}} \\ $$$${q}^{\mathrm{3}} ={q}+{c} \\ $$
