Question Number 186271 by cherokeesay last updated on 02/Feb/23

Answered by HeferH last updated on 02/Feb/23

Commented by HeferH last updated on 02/Feb/23

$${x}\:+\:\frac{{x}}{\:\sqrt{\mathrm{3}}}\:+\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left({x}\:+\:{x}\sqrt{\mathrm{3}}\right)\:=\:\mathrm{6} \\ $$$$\:\mathrm{3}{x}\:+\:\mathrm{3}{x}\sqrt{\mathrm{3}}=\:\mathrm{6}\sqrt{\mathrm{3}} \\ $$$$\:{x}\left(\mathrm{3}\:+\:\mathrm{3}\sqrt{\mathrm{3}}\right)\:=\mathrm{6}\sqrt{\mathrm{3}} \\ $$$$\:{x}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{1}\:+\:\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:\mathrm{3}−\sqrt{\mathrm{3}}\: \\ $$$$\:{x}^{\mathrm{2}} \:=\:\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:=\:\mathrm{12}−\mathrm{6}\sqrt{\mathrm{3}}\:\approx\:\mathrm{1}.\mathrm{6}\:{u}^{\mathrm{2}} \\ $$$$\: \\ $$
Commented by cherokeesay last updated on 02/Feb/23

$${Nice}\:!\:{thank}\:{you} \\ $$
Answered by mr W last updated on 02/Feb/23
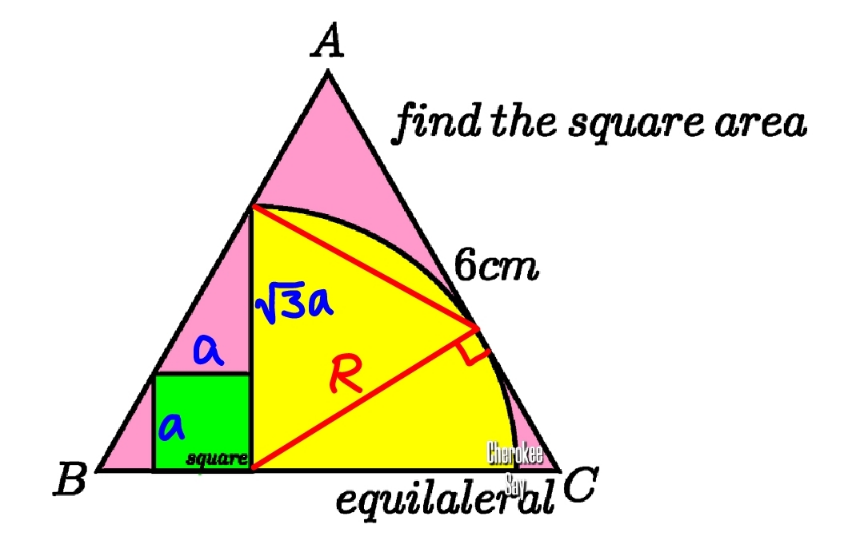
Commented by mr W last updated on 02/Feb/23

$$\frac{\mathrm{2}{R}}{\:\sqrt{\mathrm{3}}}+\frac{{R}}{\:\sqrt{\mathrm{3}}}=\mathrm{6} \\ $$$$\Rightarrow{R}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${a}+\sqrt{\mathrm{3}}{a}={R}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{1}+\sqrt{\mathrm{3}}}=\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)=\mathrm{3}−\sqrt{\mathrm{3}} \\ $$$${a}^{\mathrm{2}} =\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{6}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\approx\mathrm{1}.\mathrm{608} \\ $$
Commented by cherokeesay last updated on 02/Feb/23

$${great}\:!\:{thank}\:{you}\: \\ $$
