Menu Close

Question-186298

Tinku Tara 0 Comments
Pin




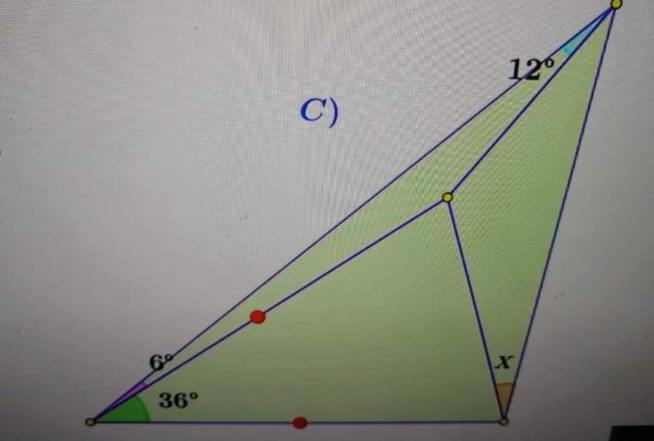
Question Number 186298 by TUN last updated on 03/Feb/23
Answered by a.lgnaoui last updated on 05/Feb/23
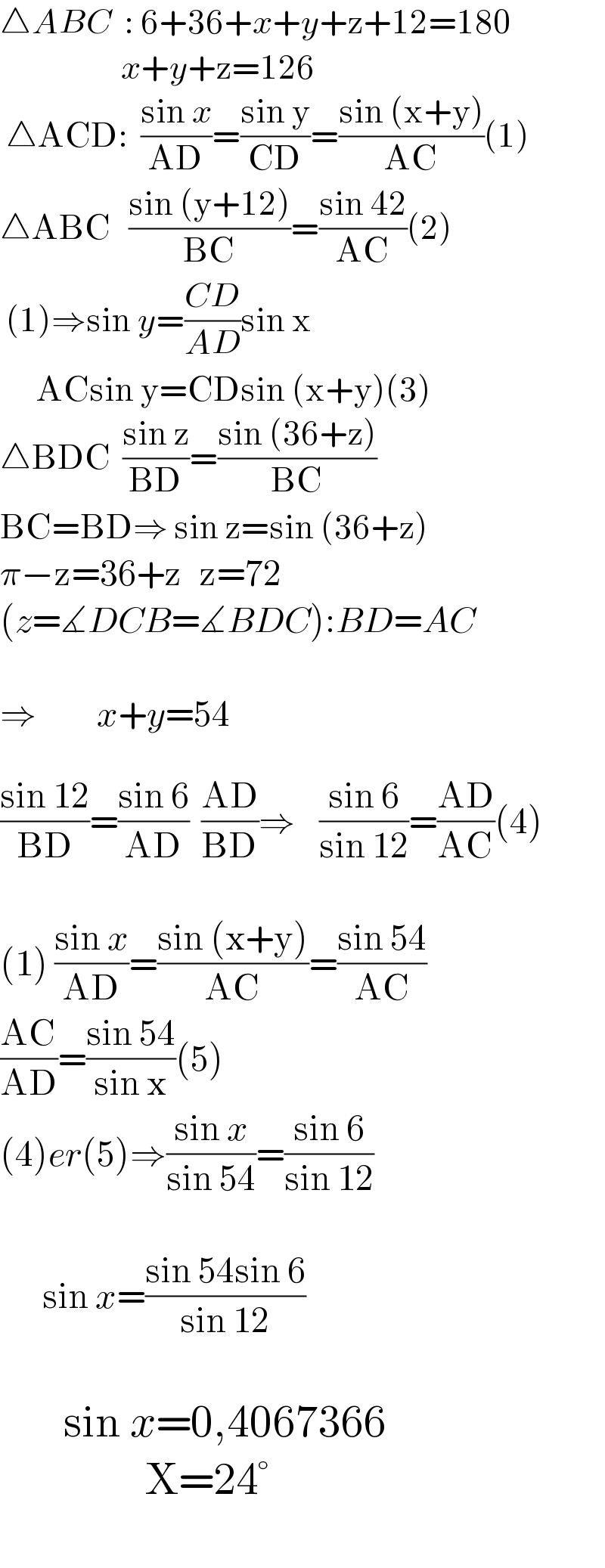
△ABC : 6+36+x+y+z+12=180 x+y+z=126 △ACD: ((sin x)/(AD))=((sin y)/(CD))=((sin (x+y))/(AC))(1) △ABC ((sin (y+12))/(BC))=((sin 42)/(AC))(2) (1)⇒sin y=((CD)/(AD))sin x ACsin y=CDsin (x+y)(3) △BDC ((sin z)/(BD))=((sin (36+z))/(BC)) BC=BD⇒ sin z=sin (36+z) π−z=36+z z=72 (z=∡DCB=∡BDC):BD=AC ⇒ x+y=54 ((sin 12)/(BD))=((sin 6)/(AD)) ((AD)/(BD))⇒ ((sin 6)/(sin 12))=((AD)/(AC))(4) (1) ((sin x)/(AD))=((sin (x+y))/(AC))=((sin 54)/(AC)) ((AC)/(AD))=((sin 54)/(sin x))(5) (4)er(5)⇒((sin x)/(sin 54))=((sin 6)/(sin 12)) sin x=((sin 54sin 6)/(sin 12)) sin x=0,4067366 X=24°
$$\bigtriangleup{ABC}\:\::\:\mathrm{6}+\mathrm{36}+{x}+{y}+\mathrm{z}+\mathrm{12}=\mathrm{180} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}+{y}+\mathrm{z}=\mathrm{126} \\ $$$$\:\bigtriangleup\mathrm{ACD}:\:\:\frac{\mathrm{sin}\:{x}}{\mathrm{AD}}=\frac{\mathrm{sin}\:\mathrm{y}}{\mathrm{CD}}=\frac{\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right)}{\mathrm{AC}}\left(\mathrm{1}\right) \\ $$$$\bigtriangleup\mathrm{ABC}\:\:\:\frac{\mathrm{sin}\:\left(\mathrm{y}+\mathrm{12}\right)}{\mathrm{BC}}=\frac{\mathrm{sin}\:\mathrm{42}}{\mathrm{AC}}\left(\mathrm{2}\right) \\ $$$$\:\left(\mathrm{1}\right)\Rightarrow\mathrm{sin}\:{y}=\frac{{CD}}{{AD}}\mathrm{sin}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\mathrm{ACsin}\:\mathrm{y}=\mathrm{CDsin}\:\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{3}\right) \\ $$$$\bigtriangleup\mathrm{BDC}\:\:\frac{\mathrm{sin}\:\mathrm{z}}{\mathrm{BD}}=\frac{\mathrm{sin}\:\left(\mathrm{36}+\mathrm{z}\right)}{\mathrm{BC}} \\ $$$$\mathrm{BC}=\mathrm{BD}\Rightarrow\:\mathrm{sin}\:\mathrm{z}=\mathrm{sin}\:\left(\mathrm{36}+\mathrm{z}\right) \\ $$$$\pi−\mathrm{z}=\mathrm{36}+\mathrm{z}\:\:\:\mathrm{z}=\mathrm{72} \\ $$$$\left({z}=\measuredangle{DCB}=\measuredangle{BDC}\right):{BD}={AC} \\ $$$$ \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:{x}+{y}=\mathrm{54} \\ $$$$ \\ $$$$\frac{\mathrm{sin}\:\mathrm{12}}{\mathrm{BD}}=\frac{\mathrm{sin}\:\mathrm{6}}{\mathrm{AD}}\:\:\frac{\mathrm{AD}}{\mathrm{BD}}\Rightarrow\:\:\:\:\frac{\mathrm{sin}\:\mathrm{6}}{\mathrm{sin}\:\mathrm{12}}=\frac{\mathrm{AD}}{\mathrm{AC}}\left(\mathrm{4}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\frac{\mathrm{sin}\:{x}}{\mathrm{AD}}=\frac{\mathrm{sin}\:\left(\mathrm{x}+\mathrm{y}\right)}{\mathrm{AC}}=\frac{\mathrm{sin}\:\mathrm{54}}{\mathrm{AC}} \\ $$$$\frac{\mathrm{AC}}{\mathrm{AD}}=\frac{\mathrm{sin}\:\mathrm{54}}{\mathrm{sin}\:\mathrm{x}}\left(\mathrm{5}\right) \\ $$$$\left(\mathrm{4}\right){er}\left(\mathrm{5}\right)\Rightarrow\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{54}}=\frac{\mathrm{sin}\:\mathrm{6}}{\mathrm{sin}\:\mathrm{12}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{sin}\:{x}=\frac{\mathrm{sin}\:\mathrm{54sin}\:\mathrm{6}}{\mathrm{sin}\:\mathrm{12}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{sin}\:{x}=\mathrm{0},\mathrm{4067366} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{X}=\mathrm{24}° \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *