Question Number 186321 by Mingma last updated on 03/Feb/23

Answered by normans last updated on 03/Feb/23
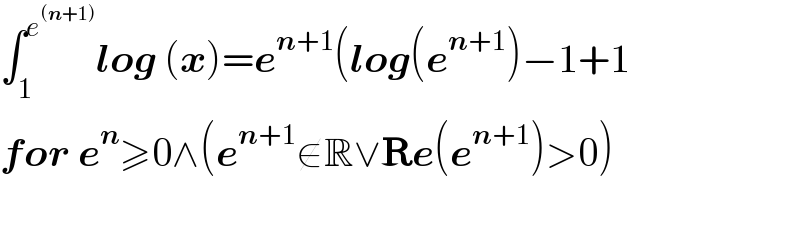
$$\int_{\mathrm{1}} ^{{e}^{\left(\boldsymbol{{n}}+\mathrm{1}\right)} } \boldsymbol{{log}}\:\left(\boldsymbol{{x}}\right)=\boldsymbol{{e}}^{\boldsymbol{{n}}+\mathrm{1}} \left(\boldsymbol{{log}}\left(\boldsymbol{{e}}^{\boldsymbol{{n}}+\mathrm{1}} \right)−\mathrm{1}+\mathrm{1}\right. \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{e}}^{\boldsymbol{{n}}} \geqslant\mathrm{0}\wedge\left(\boldsymbol{{e}}^{\boldsymbol{{n}}+\mathrm{1}} \notin\mathbb{R}\vee\boldsymbol{\mathrm{R}{e}}\left(\boldsymbol{{e}}^{\boldsymbol{{n}}+\mathrm{1}} \right)>\mathrm{0}\right) \\ $$$$ \\ $$
Commented by MJS_new last updated on 03/Feb/23
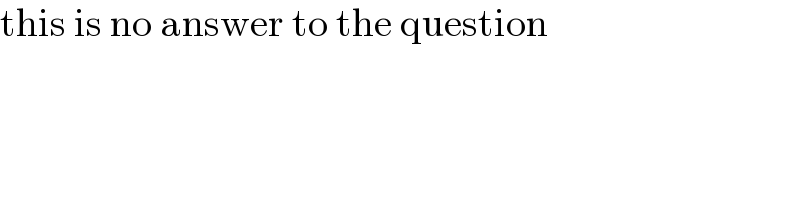
$$\mathrm{this}\:\mathrm{is}\:\mathrm{no}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{the}\:\mathrm{question} \\ $$
Answered by MJS_new last updated on 03/Feb/23
![assuming n∈N ∫_1 ^e^(n+1) ⌊ln x⌋dx= [t=ln x → dx=e^t dt] =∫_0 ^(n+1) e^t ⌊t⌋dt=0[e^t ]_0 ^1 +1[e^t ]_1 ^2 +...n[e^t ]_n ^(n+1) = =Σ_(k=0) ^n (k(e^(k+1) −e^k )) =(e−1)Σ_(k=0) ^n (ke^k ) = =(e−1)(((1+(ne−n−1)e^n )e)/((e−1)^2 ))= =ne^(n+1) −(((e^n −1)e)/(e−1))](https://www.tinkutara.com/question/Q186340.png)
$$\mathrm{assuming}\:{n}\in\mathbb{N} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{e}^{{n}+\mathrm{1}} } {\int}}\lfloor\mathrm{ln}\:{x}\rfloor{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{ln}\:{x}\:\rightarrow\:{dx}=\mathrm{e}^{{t}} {dt}\right] \\ $$$$=\underset{\mathrm{0}} {\overset{{n}+\mathrm{1}} {\int}}\mathrm{e}^{{t}} \lfloor{t}\rfloor{dt}=\mathrm{0}\left[\mathrm{e}^{{t}} \right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{1}\left[\mathrm{e}^{{t}} \right]_{\mathrm{1}} ^{\mathrm{2}} +…{n}\left[\mathrm{e}^{{t}} \right]_{{n}} ^{{n}+\mathrm{1}} = \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:\left({k}\left(\mathrm{e}^{{k}+\mathrm{1}} −\mathrm{e}^{{k}} \right)\right)\:=\left(\mathrm{e}−\mathrm{1}\right)\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({k}\mathrm{e}^{{k}} \right)\:= \\ $$$$=\left(\mathrm{e}−\mathrm{1}\right)\frac{\left(\mathrm{1}+\left({n}\mathrm{e}−{n}−\mathrm{1}\right)\mathrm{e}^{{n}} \right)\mathrm{e}}{\left(\mathrm{e}−\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$={n}\mathrm{e}^{{n}+\mathrm{1}} −\frac{\left(\mathrm{e}^{{n}} −\mathrm{1}\right)\mathrm{e}}{\mathrm{e}−\mathrm{1}} \\ $$
Answered by Mathspace last updated on 04/Feb/23
![changement lnx=t give x=e^t ⇒ I=∫_0 ^(n+1) [t]e^t dt =Σ_(k=0) ^(n−1) ∫_k ^(k+1) k e^t dt =Σ_(k=0) ^(n−1) k(e^(k+1) −e^k ) =(e−1)Σ_(k=1) ^(n−1) ke^k f(x)=Σ_(k=0) ^(n−1) x^k =((x^n −1)/(x−1)) for x≠1 f^′ (x)=Σ_(k=1) ^(n−1) kx^(k−1) ⇒ xf^′ (x)=Σ_(k=1) ^(n−1) k x^k =x.((nx^(n−1) (x−1)−(x^n −1))/((x−1)^2 )) =x.((nx^n −nx^(n−1) −x^n +1)/((x−1)^2 )) =x.(((n−1)x^n −nx^(n−1) +1)/((x−1)^2 )) =(((n−1)x^(n+1) −nx^n +x)/((x−1)^2 )) x=e ⇒Σ_(k=1) ^(n−1) ke^k =(((n−1)e^(n+1) −ne^n +e)/((e−1)^2 )) ⇒ ⇒I=(e−1).(((n−1)e^(n+1) −ne^n +e)/((e−1)^2 )) =(((n−1)e^(n+1) −ne^n +e)/(e−1))](https://www.tinkutara.com/question/Q186423.png)
$${changement}\:{lnx}={t}\:{give}\:{x}={e}^{{t}} \Rightarrow \\ $$$${I}=\int_{\mathrm{0}} ^{{n}+\mathrm{1}} \left[{t}\right]{e}^{{t}} {dt} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \int_{{k}} ^{{k}+\mathrm{1}} {k}\:{e}^{{t}} {dt} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {k}\left({e}^{{k}+\mathrm{1}} −{e}^{{k}} \right) \\ $$$$=\left({e}−\mathrm{1}\right)\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {ke}^{{k}} \\ $$$${f}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {x}^{{k}} \:=\frac{{x}^{{n}} −\mathrm{1}}{{x}−\mathrm{1}}\:{for}\:{x}\neq\mathrm{1} \\ $$$${f}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {kx}^{{k}−\mathrm{1}} \:\Rightarrow \\ $$$${xf}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {k}\:{x}^{{k}} \\ $$$$={x}.\frac{{nx}^{{n}−\mathrm{1}} \left({x}−\mathrm{1}\right)−\left({x}^{{n}} −\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$={x}.\frac{{nx}^{{n}} −{nx}^{{n}−\mathrm{1}} −{x}^{{n}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$={x}.\frac{\left({n}−\mathrm{1}\right){x}^{{n}} −{nx}^{{n}−\mathrm{1}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left({n}−\mathrm{1}\right){x}^{{n}+\mathrm{1}} −{nx}^{{n}} +{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${x}={e}\:\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {ke}^{{k}} \\ $$$$=\frac{\left({n}−\mathrm{1}\right){e}^{{n}+\mathrm{1}} −{ne}^{{n}} +{e}}{\left({e}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\Rightarrow{I}=\left({e}−\mathrm{1}\right).\frac{\left({n}−\mathrm{1}\right){e}^{{n}+\mathrm{1}} −{ne}^{{n}} +{e}}{\left({e}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left({n}−\mathrm{1}\right){e}^{{n}+\mathrm{1}} −{ne}^{{n}} +{e}}{{e}−\mathrm{1}} \\ $$
