Question Number 186323 by Rupesh123 last updated on 03/Feb/23
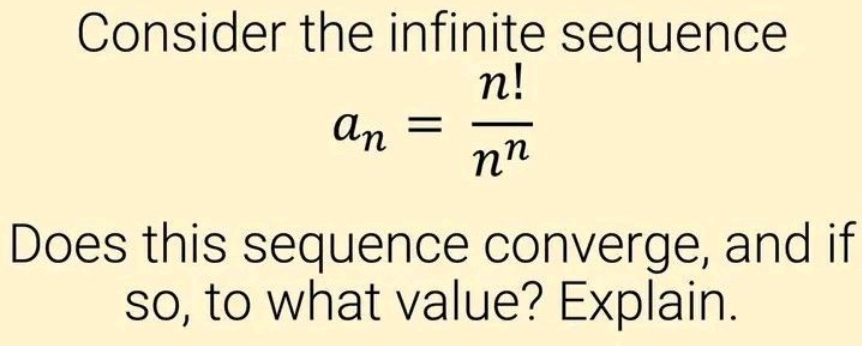
Commented by Frix last updated on 03/Feb/23

$${n}!\sim\frac{{n}^{{n}} }{\mathrm{e}^{{n}} }\sqrt{\mathrm{2}\pi{n}} \\ $$$${a}_{{n}} \sim\frac{\sqrt{\mathrm{2}\pi{n}}}{\mathrm{e}^{{n}} } \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} \:=\mathrm{0} \\ $$
Answered by JDamian last updated on 03/Feb/23

$$\underline{\mathrm{just}\:\mathrm{a}\:\mathrm{bit}\:\mathrm{of}\:\mathrm{thinking}} \\ $$$$\mathrm{both}\:\mathrm{numerator}\:\mathrm{and}\:\mathrm{denominator}\:\mathrm{are} \\ $$$$\mathrm{products}\:\mathrm{of}\:\boldsymbol{{n}}\:\mathrm{factors} \\ $$$${a}_{{n}} =\frac{\cancel{{n}}}{\cancel{{n}}}\:\centerdot\:\frac{{n}−\mathrm{1}}{{n}}\:\centerdot\:\frac{{n}−\mathrm{2}}{{n}}\:\centerdot\centerdot\centerdot\:\frac{\mathrm{2}}{{n}}\:\centerdot\:\frac{\mathrm{1}}{{n}} \\ $$$$\mathrm{every}\:\mathrm{fraction}\:\mathrm{is}\:<\mathrm{1} \\ $$$${a}_{{n}} <\mathrm{1}\:\:\:\:\:\forall{n}>\mathrm{1} \\ $$$$\mathrm{Denominator}\:\mathrm{grows}\:\mathrm{faster}\:\mathrm{than}\:\mathrm{numerator} \\ $$$$\mathrm{because}\:\:\:\mathrm{n}^{\mathrm{n}} >\mathrm{n}!\:\:\:\forall{n}>\mathrm{1} \\ $$
