Question Number 186345 by ajfour last updated on 03/Feb/23
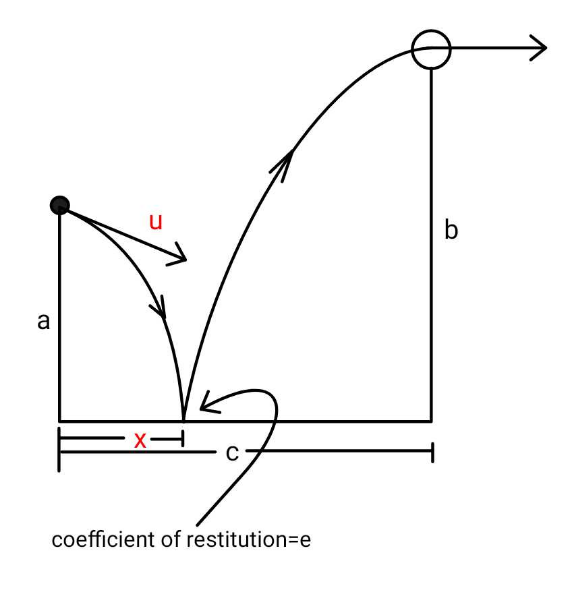
Answered by mr W last updated on 04/Feb/23
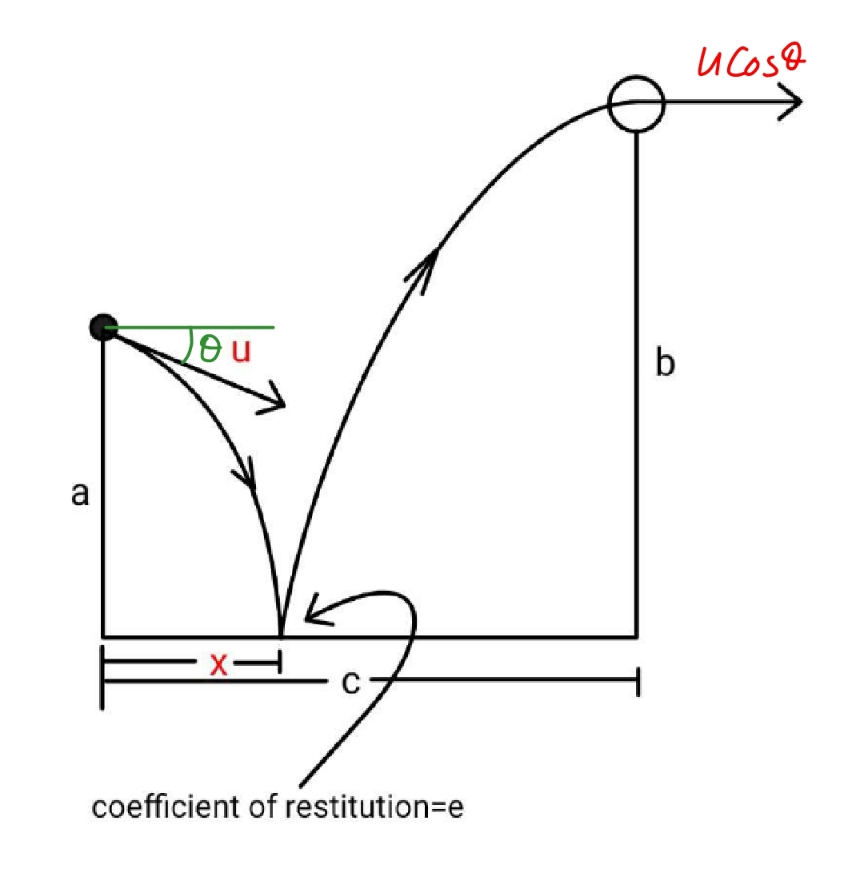
Commented by mr W last updated on 04/Feb/23
/( 2b(√((1/e^2 )−(a/b)))))−1)(√((2b)/g)) (a/b)= (2(√((1/e^2 )−(a/b))) +((c tan θ)/( 2b(√((1/e^2 )−(a/b)))))−1)(((c tan θ)/( 2b(√((1/e^2 )−(a/b)))))−1) let μ=(a/b), λ=2(√((1/e^2 )−(a/b))), ξ=((c tan θ)/(2b(√((1/e^2 )−(a/b)))))−1 μ= (λ +ξ)ξ ξ^2 +λξ−μ=0 ⇒ξ=(((√(λ^2 +4μ))−λ)/2) ((c tan θ)/(2b(√((1/e^2 )−(a/b)))))−1=(1/e)−(√((1/e^2 )−(a/b))) ⇒tan θ=((2b)/c)(1+(1/e)−(√((1/e^2 )−(a/b))))(√((1/e^2 )−(a/b))) ⇒u=((√(2gb))/(sin θ))(√((1/e^2 )−(a/b))) x=c−u cos θ t_2 x=c−((2b)/(tan θ))(√((1/e^2 )−(a/b))) ⇒x=c(1−(1/(1+(1/e)−(√((1/e^2 )−(a/b))))))](https://www.tinkutara.com/question/Q186378.png)
$$\sqrt{\mathrm{2}{gb}}={e}\sqrt{\left({u}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} +\mathrm{2}{ga}} \\ $$$$\Rightarrow{u}\:\mathrm{sin}\:\theta=\sqrt{\mathrm{2}{gb}\left(\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}\right)} \\ $$$${t}=\frac{{c}}{{u}\:\mathrm{cos}\:\theta}=\frac{{c}\:\mathrm{tan}\:\theta}{{u}\:\mathrm{sin}\:\theta}=\frac{{c}\:\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{2}{gb}\left(\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}\right)}} \\ $$$${b}=\frac{{gt}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow{t}_{\mathrm{2}} =\sqrt{\frac{\mathrm{2}{b}}{{g}}} \\ $$$${t}_{\mathrm{1}} ={t}−{t}_{\mathrm{2}} =\frac{{c}\:\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{2}{gb}\left(\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}\right)}}−\sqrt{\frac{\mathrm{2}{b}}{{g}}} \\ $$$$\Rightarrow{t}_{\mathrm{1}} =\left(\frac{{c}\:\mathrm{tan}\:\theta}{\:\mathrm{2}{b}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{2}{b}}{{g}}} \\ $$$${a}={u}\:\mathrm{sin}\:\theta\:{t}_{\mathrm{1}} +\frac{{gt}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$${a}=\left[\sqrt{\mathrm{2}{gb}\left(\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}\right)}\:+\frac{{g}}{\mathrm{2}}\left(\frac{{c}\:\mathrm{tan}\:\theta}{\:\mathrm{2}{b}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{2}{b}}{{g}}}\right]\left(\frac{{c}\:\mathrm{tan}\:\theta}{\:\mathrm{2}{b}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{2}{b}}{{g}}} \\ $$$$\frac{{a}}{{b}}=\:\left(\mathrm{2}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}\:+\frac{{c}\:\mathrm{tan}\:\theta}{\:\mathrm{2}{b}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}}−\mathrm{1}\right)\left(\frac{{c}\:\mathrm{tan}\:\theta}{\:\mathrm{2}{b}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}}−\mathrm{1}\right) \\ $$$${let}\:\mu=\frac{{a}}{{b}},\:\lambda=\mathrm{2}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}},\:\xi=\frac{{c}\:\mathrm{tan}\:\theta}{\mathrm{2}{b}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}}−\mathrm{1} \\ $$$$\mu=\:\left(\lambda\:+\xi\right)\xi \\ $$$$\xi^{\mathrm{2}} +\lambda\xi−\mu=\mathrm{0} \\ $$$$\Rightarrow\xi=\frac{\sqrt{\lambda^{\mathrm{2}} +\mathrm{4}\mu}−\lambda}{\mathrm{2}} \\ $$$$\frac{{c}\:\mathrm{tan}\:\theta}{\mathrm{2}{b}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}}−\mathrm{1}=\frac{\mathrm{1}}{{e}}−\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{2}{b}}{{c}}\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}−\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}\right)\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}} \\ $$$$\Rightarrow{u}=\frac{\sqrt{\mathrm{2}{gb}}}{\mathrm{sin}\:\theta}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}} \\ $$$${x}={c}−{u}\:\mathrm{cos}\:\theta\:{t}_{\mathrm{2}} \\ $$$${x}={c}−\frac{\mathrm{2}{b}}{\mathrm{tan}\:\theta}\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}} \\ $$$$\Rightarrow{x}={c}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{e}}−\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}}\right) \\ $$
Commented by mr W last updated on 04/Feb/23
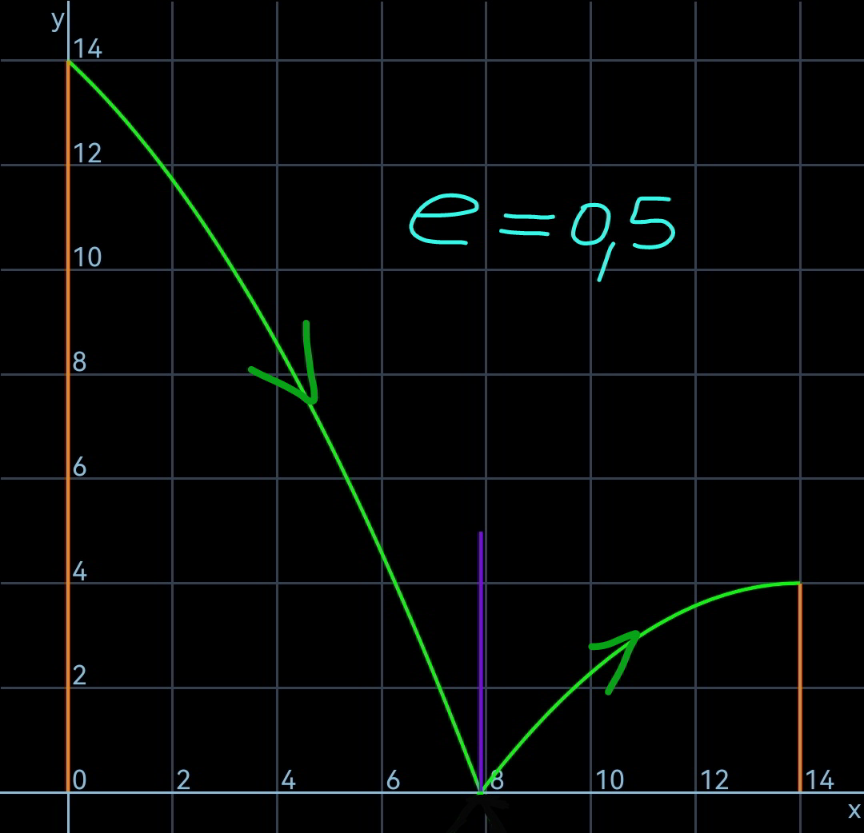
Commented by mr W last updated on 04/Feb/23
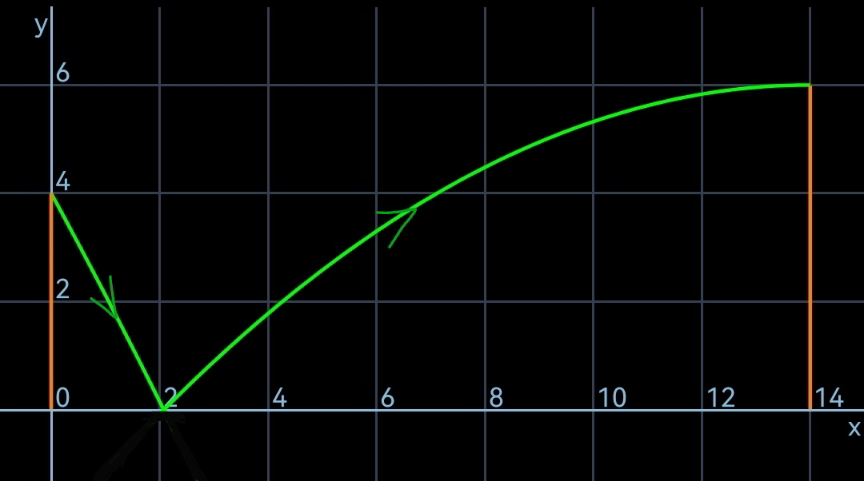
Commented by ajfour last updated on 04/Feb/23
$${Thank}\:{you}\:{sir},\:{thats}\:{superb} \\ $$$${agreement}.\:{I}\:{shall}\:{attemt}\:{too}. \\ $$
