Question Number 186399 by normans last updated on 04/Feb/23

Answered by mr W last updated on 04/Feb/23

Commented by mr W last updated on 04/Feb/23
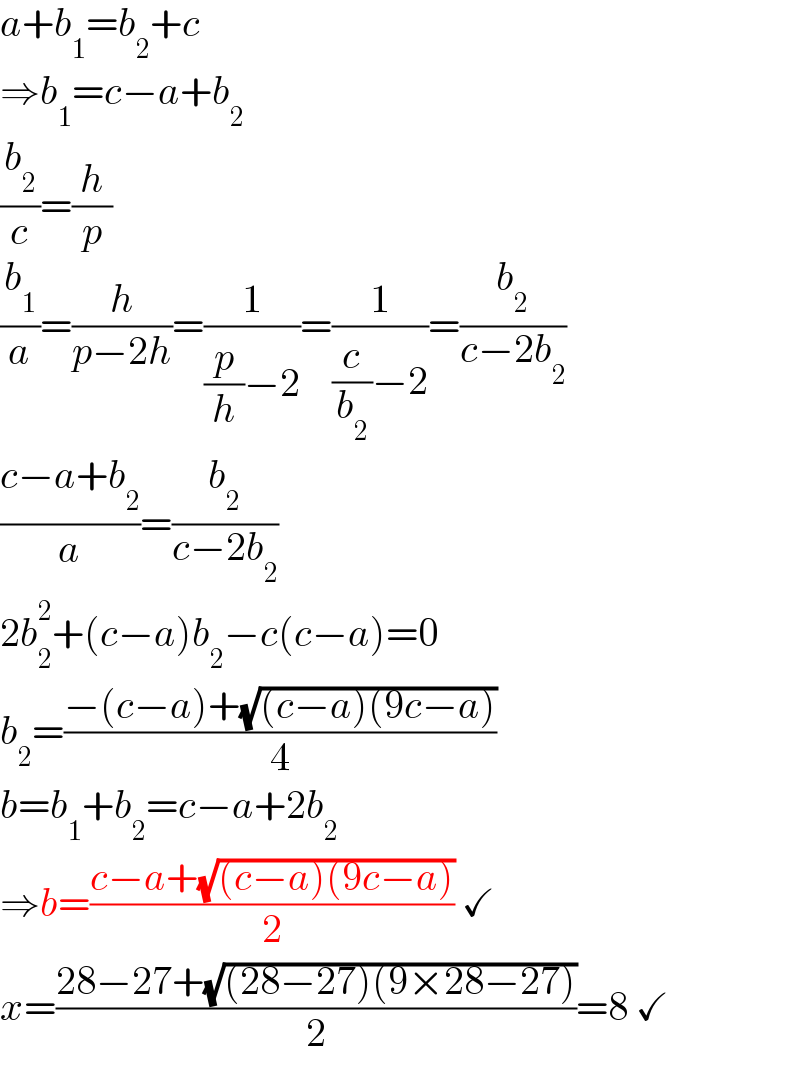
$${a}+{b}_{\mathrm{1}} ={b}_{\mathrm{2}} +{c} \\ $$$$\Rightarrow{b}_{\mathrm{1}} ={c}−{a}+{b}_{\mathrm{2}} \\ $$$$\frac{{b}_{\mathrm{2}} }{{c}}=\frac{{h}}{{p}} \\ $$$$\frac{{b}_{\mathrm{1}} }{{a}}=\frac{{h}}{{p}−\mathrm{2}{h}}=\frac{\mathrm{1}}{\frac{{p}}{{h}}−\mathrm{2}}=\frac{\mathrm{1}}{\frac{{c}}{{b}_{\mathrm{2}} }−\mathrm{2}}=\frac{{b}_{\mathrm{2}} }{{c}−\mathrm{2}{b}_{\mathrm{2}} } \\ $$$$\frac{{c}−{a}+{b}_{\mathrm{2}} }{{a}}=\frac{{b}_{\mathrm{2}} }{{c}−\mathrm{2}{b}_{\mathrm{2}} } \\ $$$$\mathrm{2}{b}_{\mathrm{2}} ^{\mathrm{2}} +\left({c}−{a}\right){b}_{\mathrm{2}} −{c}\left({c}−{a}\right)=\mathrm{0} \\ $$$${b}_{\mathrm{2}} =\frac{−\left({c}−{a}\right)+\sqrt{\left({c}−{a}\right)\left(\mathrm{9}{c}−{a}\right)}}{\mathrm{4}} \\ $$$${b}={b}_{\mathrm{1}} +{b}_{\mathrm{2}} ={c}−{a}+\mathrm{2}{b}_{\mathrm{2}} \\ $$$$\Rightarrow{b}=\frac{{c}−{a}+\sqrt{\left({c}−{a}\right)\left(\mathrm{9}{c}−{a}\right)}}{\mathrm{2}}\:\checkmark \\ $$$${x}=\frac{\mathrm{28}−\mathrm{27}+\sqrt{\left(\mathrm{28}−\mathrm{27}\right)\left(\mathrm{9}×\mathrm{28}−\mathrm{27}\right)}}{\mathrm{2}}=\mathrm{8}\:\checkmark \\ $$
Commented by normans last updated on 04/Feb/23
$$\boldsymbol{{thank}}\:\boldsymbol{{hou}},\:\boldsymbol{{great}}\:\boldsymbol{{S}}{ir} \\ $$
