Question Number 186416 by ajfour last updated on 04/Feb/23

Commented by ajfour last updated on 04/Feb/23

$${Q}.\:\mathrm{186345} \\ $$
Answered by ajfour last updated on 04/Feb/23
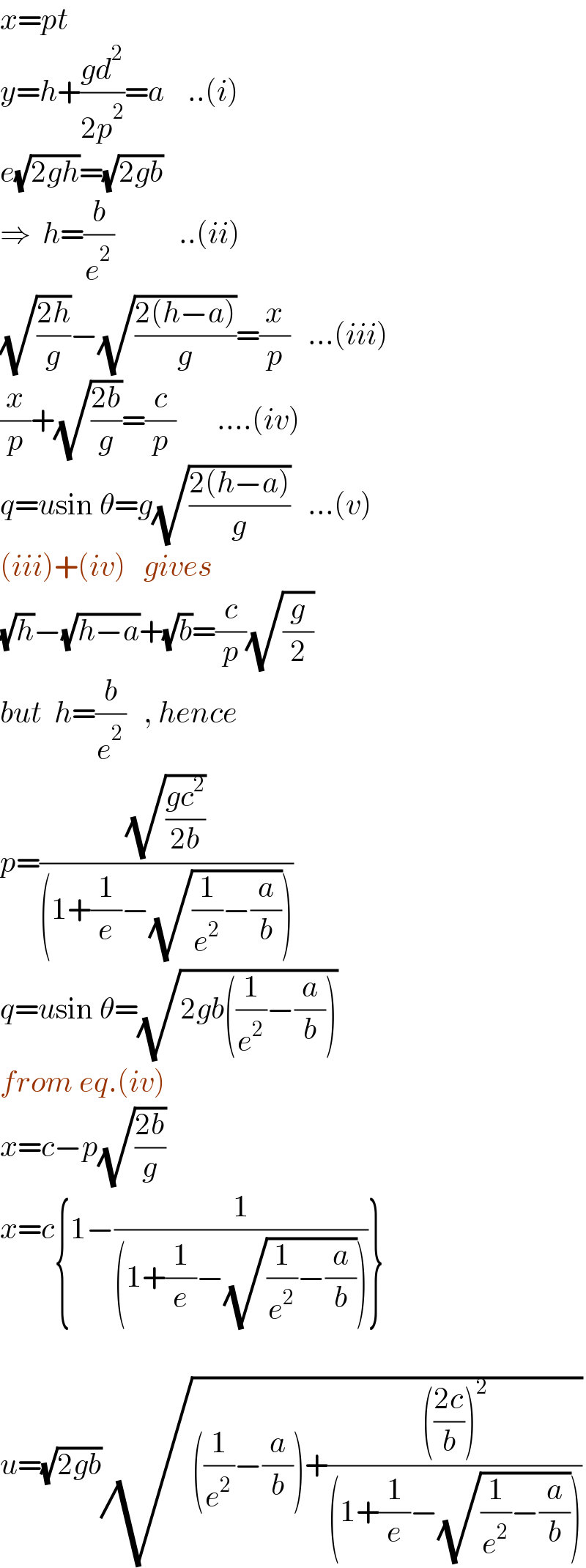
$${x}={pt} \\ $$$${y}={h}+\frac{{gd}^{\mathrm{2}} }{\mathrm{2}{p}^{\mathrm{2}} }={a}\:\:\:\:..\left({i}\right) \\ $$$${e}\sqrt{\mathrm{2}{gh}}=\sqrt{\mathrm{2}{gb}} \\ $$$$\Rightarrow\:\:{h}=\frac{{b}}{{e}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:..\left({ii}\right) \\ $$$$\sqrt{\frac{\mathrm{2}{h}}{{g}}}−\sqrt{\frac{\mathrm{2}\left({h}−{a}\right)}{{g}}}=\frac{{x}}{{p}}\:\:\:…\left({iii}\right) \\ $$$$\frac{{x}}{{p}}+\sqrt{\frac{\mathrm{2}{b}}{{g}}}=\frac{{c}}{{p}}\:\:\:\:\:\:\:….\left({iv}\right) \\ $$$${q}={u}\mathrm{sin}\:\theta={g}\sqrt{\frac{\mathrm{2}\left({h}−{a}\right)}{{g}}}\:\:\:…\left({v}\right) \\ $$$$\left({iii}\right)+\left({iv}\right)\:\:\:{gives} \\ $$$$\sqrt{{h}}−\sqrt{{h}−{a}}+\sqrt{{b}}=\frac{{c}}{{p}}\sqrt{\frac{{g}}{\mathrm{2}}} \\ $$$${but}\:\:{h}=\frac{{b}}{{e}^{\mathrm{2}} }\:\:\:,\:{hence} \\ $$$${p}=\frac{\sqrt{\frac{{gc}^{\mathrm{2}} }{\mathrm{2}{b}}}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}−\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}\right)} \\ $$$${q}={u}\mathrm{sin}\:\theta=\sqrt{\mathrm{2}{gb}\left(\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}\right)} \\ $$$${from}\:{eq}.\left({iv}\right) \\ $$$${x}={c}−{p}\sqrt{\frac{\mathrm{2}{b}}{{g}}} \\ $$$${x}={c}\left\{\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}−\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}\right)}\right\} \\ $$$$ \\ $$$${u}=\sqrt{\mathrm{2}{gb}}\sqrt{\left(\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}\right)+\frac{\left(\frac{\mathrm{2}{c}}{{b}}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\frac{\mathrm{1}}{{e}}−\sqrt{\frac{\mathrm{1}}{{e}^{\mathrm{2}} }−\frac{{a}}{{b}}}\right)}} \\ $$
Commented by mr W last updated on 04/Feb/23
$${great}\:{solution}\:{sir}! \\ $$
