Question Number 186439 by ajfour last updated on 04/Feb/23

Commented by ajfour last updated on 04/Feb/23

$${If}\:{inside}\:{the}\:{fixed}\:{hollow}\:{cone}, \\ $$$${the}\:{solid}\:{ball}\:{of}\:{radius}\:{r}\:{revolves} \\ $$$${sliding}\:{frictionlessly}\:{along}\:{the} \\ $$$${lateral}\:{side}\:{and}\:{the}\:{base}\:{with} \\ $$$${angular}\:{velocity}\:\omega,\:{then}\:{find}\:{the} \\ $$$${normal}\:{reaction}\:{forces}\:{it}\:{is} \\ $$$${exerted}\:{upon}\:{by}\:{the}\:{ground}\:{and} \\ $$$${the}\:{lateral}\:{side}. \\ $$
Answered by mr W last updated on 04/Feb/23

Commented by mr W last updated on 04/Feb/23
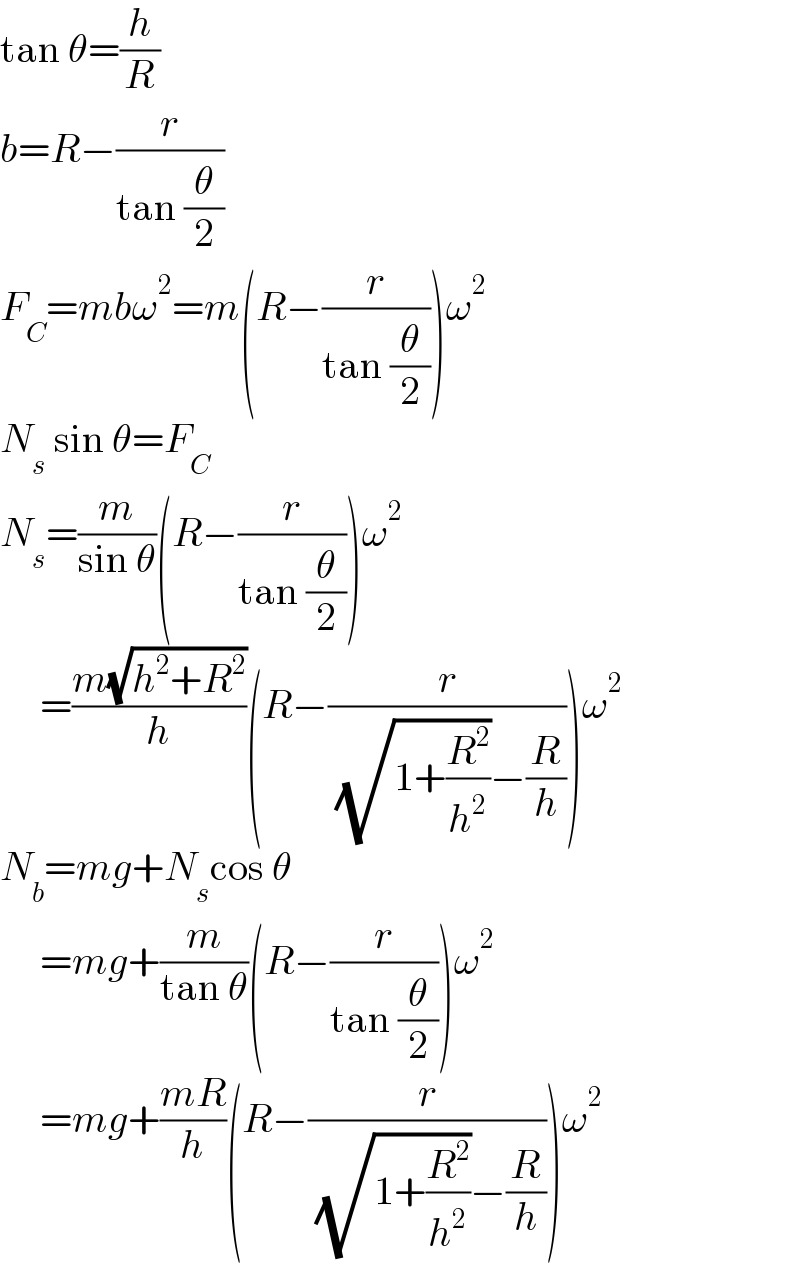
$$\mathrm{tan}\:\theta=\frac{{h}}{{R}} \\ $$$${b}={R}−\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$${F}_{{C}} ={mb}\omega^{\mathrm{2}} ={m}\left({R}−\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}\right)\omega^{\mathrm{2}} \\ $$$${N}_{{s}} \:\mathrm{sin}\:\theta={F}_{{C}} \\ $$$${N}_{{s}} =\frac{{m}}{\mathrm{sin}\:\theta}\left({R}−\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}\right)\omega^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{{m}\sqrt{{h}^{\mathrm{2}} +{R}^{\mathrm{2}} }}{{h}}\left({R}−\frac{{r}}{\:\sqrt{\mathrm{1}+\frac{{R}^{\mathrm{2}} }{{h}^{\mathrm{2}} }}−\frac{{R}}{{h}}}\right)\omega^{\mathrm{2}} \\ $$$${N}_{{b}} ={mg}+{N}_{{s}} \mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:={mg}+\frac{{m}}{\mathrm{tan}\:\theta}\left({R}−\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}\right)\omega^{\mathrm{2}} \\ $$$$\:\:\:\:\:={mg}+\frac{{mR}}{{h}}\left({R}−\frac{{r}}{\:\sqrt{\mathrm{1}+\frac{{R}^{\mathrm{2}} }{{h}^{\mathrm{2}} }}−\frac{{R}}{{h}}}\right)\omega^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 04/Feb/23
$${pretty}\:{smooth}\:{n}\:{elegant}\:{solution}. \\ $$$${Thank}\:{you}\:{sir}! \\ $$
