Question Number 186527 by Mingma last updated on 05/Feb/23
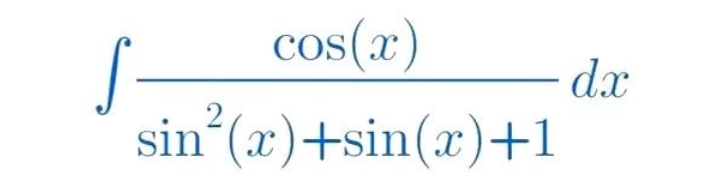
Answered by ARUNG_Brandon_MBU last updated on 05/Feb/23
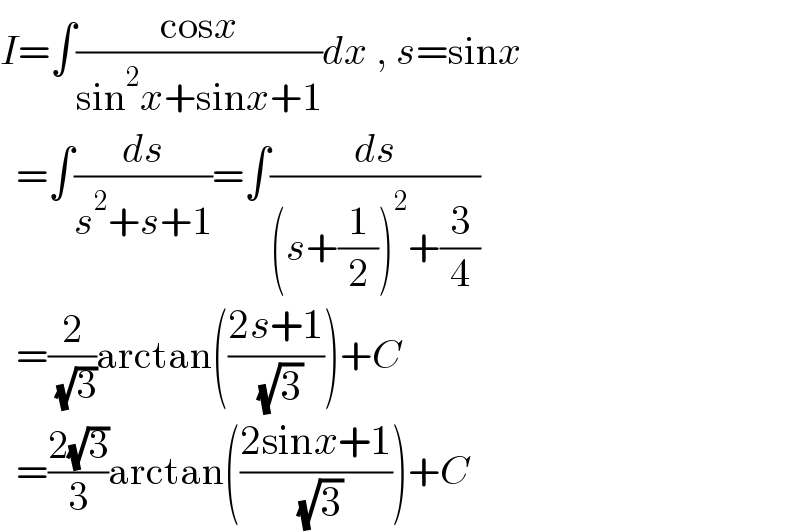
$${I}=\int\frac{\mathrm{cos}{x}}{\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{sin}{x}+\mathrm{1}}{dx}\:,\:{s}=\mathrm{sin}{x} \\ $$$$\:\:=\int\frac{{ds}}{{s}^{\mathrm{2}} +{s}+\mathrm{1}}=\int\frac{{ds}}{\left({s}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\:\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2}{s}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{C} \\ $$$$\:\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\left(\frac{\mathrm{2sin}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{C} \\ $$
Commented by aba last updated on 05/Feb/23
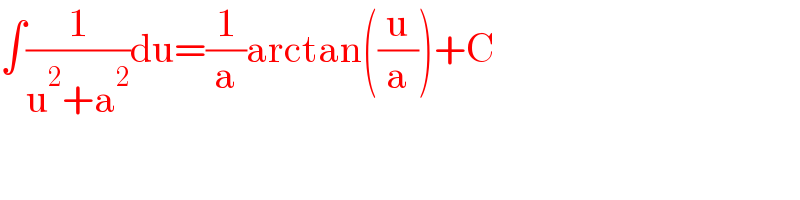
$$\int\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\mathrm{du}=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{arctan}\left(\frac{\mathrm{u}}{\mathrm{a}}\right)+\mathrm{C} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 05/Feb/23
Thanks.
Answered by aba last updated on 05/Feb/23
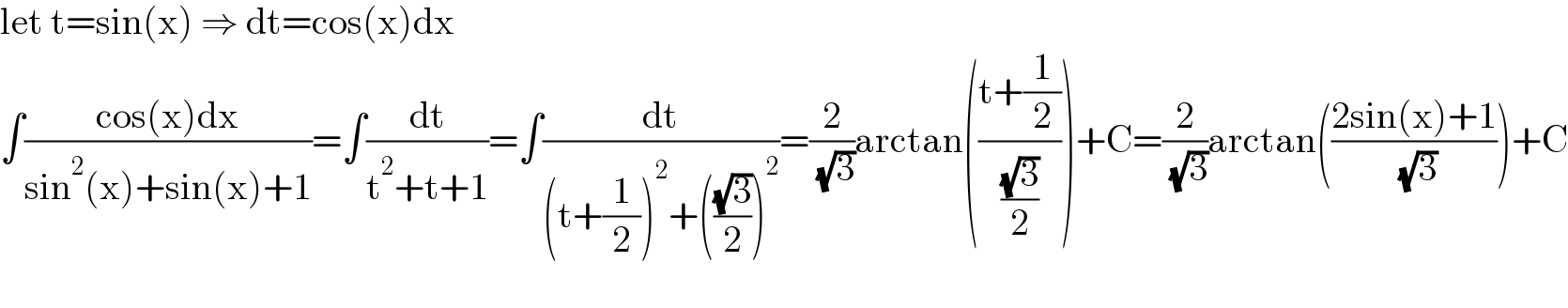
$$\mathrm{let}\:\mathrm{t}=\mathrm{sin}\left(\mathrm{x}\right)\:\Rightarrow\:\mathrm{dt}=\mathrm{cos}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\int\frac{\mathrm{cos}\left(\mathrm{x}\right)\mathrm{dx}}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{sin}\left(\mathrm{x}\right)+\mathrm{1}}=\int\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{1}}=\int\frac{\mathrm{dt}}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)+\mathrm{C}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2sin}\left(\mathrm{x}\right)+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{C} \\ $$$$ \\ $$
