Question Number 186594 by mr W last updated on 06/Feb/23
Commented by mr W last updated on 06/Feb/23
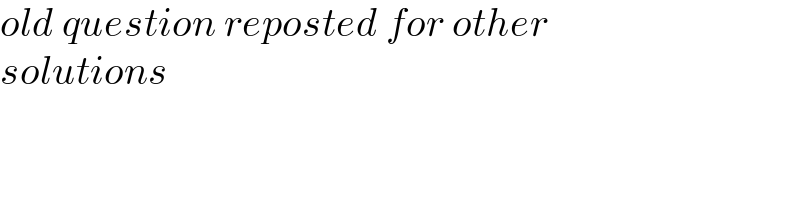
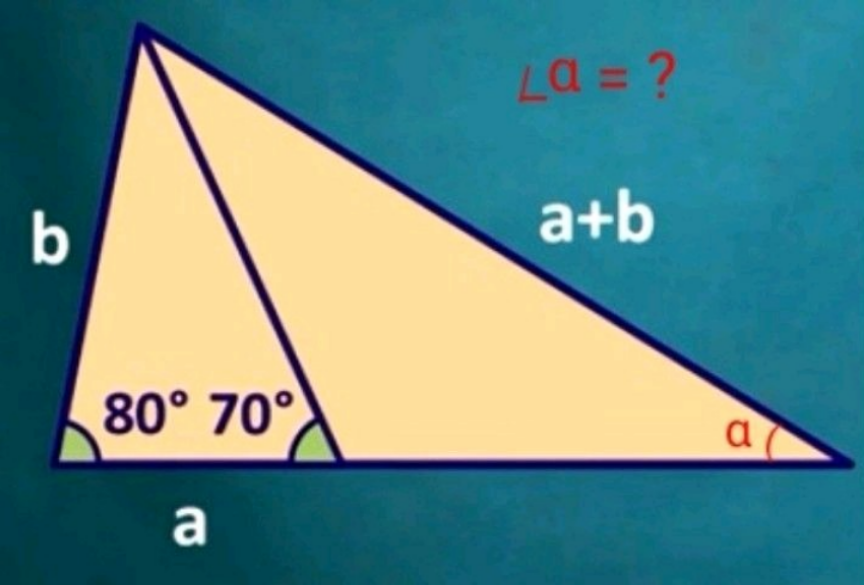
$${old}\:{question}\:{reposted}\:{for}\:{other}\: \\ $$$${solutions} \\ $$
Answered by CElcedricjunior last updated on 06/Feb/23
![(c/(sin𝛂))=((a+b)/(sin(110))) or (b/(sin70))=(c/(sin80)) =>c=((bsin80)/(sin70)) <=>((bsin80)/(sin𝛂sin70))=((a+b)/(sin110)) ★moivre =>𝛂=sin^(−1) [(b/((a+b)))((sin(80)×sin(110))/(sin(70)))] ■cedric junior](https://www.tinkutara.com/question/Q186598.png)
$$\frac{\boldsymbol{{c}}}{\boldsymbol{{sin}\alpha}}=\frac{\boldsymbol{{a}}+\boldsymbol{{b}}}{\boldsymbol{{sin}}\left(\mathrm{110}\right)}\:\boldsymbol{{or}}\:\frac{\boldsymbol{{b}}}{\boldsymbol{{sin}}\mathrm{70}}=\frac{\boldsymbol{{c}}}{\boldsymbol{{sin}}\mathrm{80}} \\ $$$$=>\boldsymbol{{c}}=\frac{\boldsymbol{{bsin}}\mathrm{80}}{\boldsymbol{{sin}}\mathrm{70}} \\ $$$$<=>\frac{\boldsymbol{{bsin}}\mathrm{80}}{\boldsymbol{{sin}\alpha{sin}}\mathrm{70}}=\frac{\boldsymbol{{a}}+\boldsymbol{{b}}}{\boldsymbol{{sin}}\mathrm{110}}\:\bigstar\boldsymbol{{moivre}}\:\: \\ $$$$=>\boldsymbol{\alpha}=\boldsymbol{{sin}}^{−\mathrm{1}} \left[\frac{\boldsymbol{{b}}}{\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)}\frac{\boldsymbol{{sin}}\left(\mathrm{80}\right)×\boldsymbol{{sin}}\left(\mathrm{110}\right)}{\boldsymbol{{sin}}\left(\mathrm{70}\right)}\right]\:\blacksquare\boldsymbol{{cedric}}\:\boldsymbol{{junior}} \\ $$$$ \\ $$
Answered by HeferH last updated on 06/Feb/23
Commented by HeferH last updated on 06/Feb/23

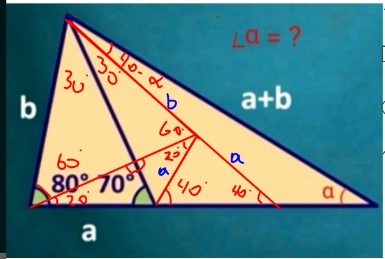
$$\:\mathrm{70}°\:>\alpha\:\Rightarrow \\ $$$$\alpha\:\neq\mathrm{140}°\:\Rightarrow \\ $$$$\:\alpha\:=\:\mathrm{40}°\: \\ $$
Answered by ajfour last updated on 06/Feb/23
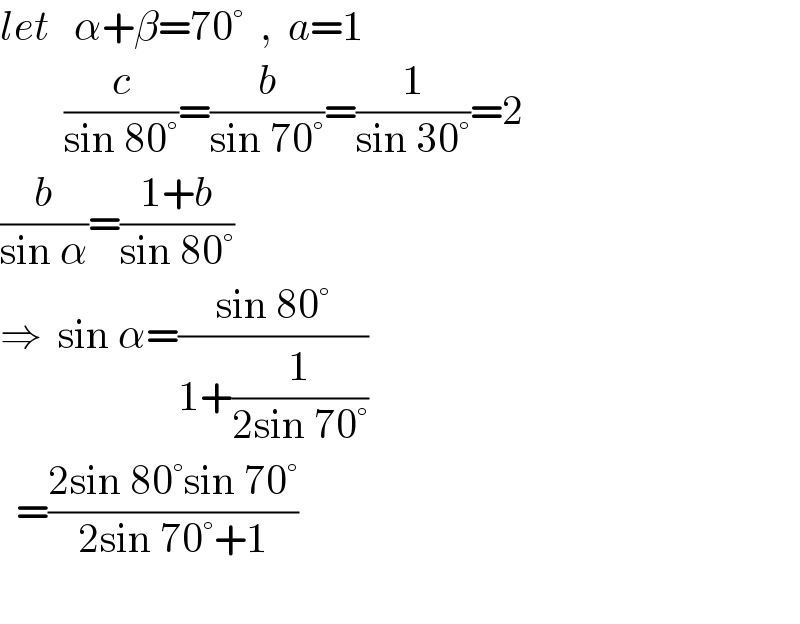
$${let}\:\:\:\alpha+\beta=\mathrm{70}°\:\:,\:\:{a}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\frac{{c}}{\mathrm{sin}\:\mathrm{80}°}=\frac{{b}}{\mathrm{sin}\:\mathrm{70}°}=\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{30}°}=\mathrm{2} \\ $$$$\frac{{b}}{\mathrm{sin}\:\alpha}=\frac{\mathrm{1}+{b}}{\mathrm{sin}\:\mathrm{80}°} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\alpha=\frac{\mathrm{sin}\:\mathrm{80}°}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2sin}\:\mathrm{70}°}} \\ $$$$\:\:=\frac{\mathrm{2sin}\:\mathrm{80}°\mathrm{sin}\:\mathrm{70}°}{\mathrm{2sin}\:\mathrm{70}°+\mathrm{1}} \\ $$$$ \\ $$
Answered by Frix last updated on 06/Feb/23
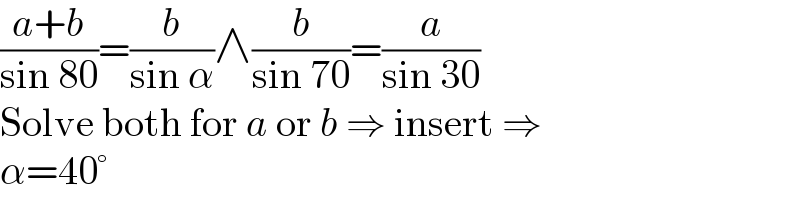
$$\frac{{a}+{b}}{\mathrm{sin}\:\mathrm{80}}=\frac{{b}}{\mathrm{sin}\:\alpha}\wedge\frac{{b}}{\mathrm{sin}\:\mathrm{70}}=\frac{{a}}{\mathrm{sin}\:\mathrm{30}} \\ $$$$\mathrm{Solve}\:\mathrm{both}\:\mathrm{for}\:{a}\:\mathrm{or}\:{b}\:\Rightarrow\:\mathrm{insert}\:\Rightarrow \\ $$$$\alpha=\mathrm{40}° \\ $$
Answered by mr W last updated on 07/Feb/23

Commented by mr W last updated on 07/Feb/23
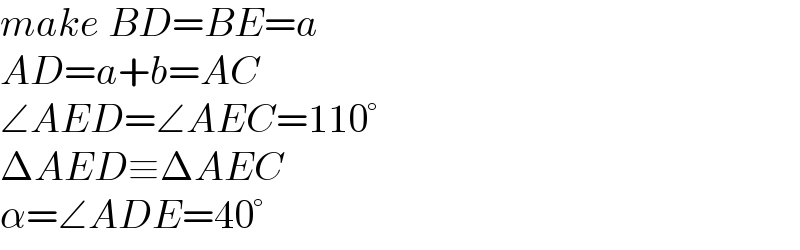
$${make}\:{BD}={BE}={a} \\ $$$${AD}={a}+{b}={AC} \\ $$$$\angle{AED}=\angle{AEC}=\mathrm{110}° \\ $$$$\Delta{AED}\equiv\Delta{AEC} \\ $$$$\alpha=\angle{ADE}=\mathrm{40}° \\ $$
