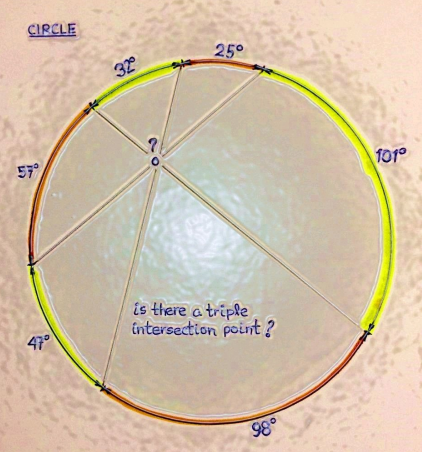
Question Number 186737 by Rupesh123 last updated on 09/Feb/23
Commented by Frix last updated on 09/Feb/23
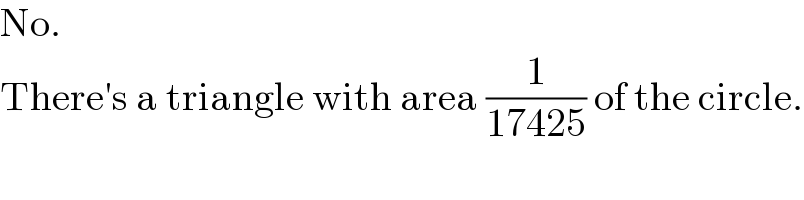
$$\mathrm{No}. \\ $$$$\mathrm{There}'\mathrm{s}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{with}\:\mathrm{area}\:\frac{\mathrm{1}}{\mathrm{17425}}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}. \\ $$
Answered by mr W last updated on 09/Feb/23
Commented by mr W last updated on 09/Feb/23

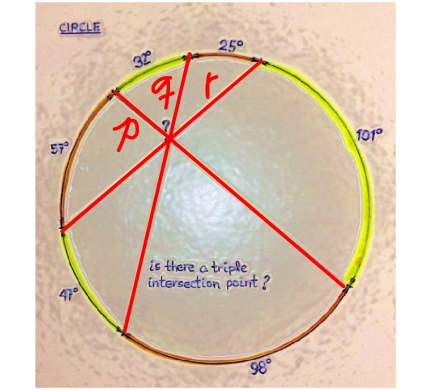
$$\mathrm{57}+\mathrm{32}+\mathrm{25}+\mathrm{101}+\mathrm{98}+\mathrm{47}=\mathrm{360}\:\checkmark \\ $$$$\frac{{q}}{{p}}=\frac{\mathrm{sin}\:\frac{\mathrm{25}+\mathrm{101}}{\mathrm{2}}}{\mathrm{sin}\:\frac{\mathrm{57}+\mathrm{47}}{\mathrm{2}}}=\frac{\mathrm{sin}\:\mathrm{63}}{\mathrm{sin}\:\mathrm{52}} \\ $$$$\frac{{p}}{{r}}=\frac{\mathrm{sin}\:\frac{\mathrm{57}}{\mathrm{2}}}{\mathrm{sin}\:\frac{\mathrm{101}}{\mathrm{2}}}=\frac{\mathrm{sin}\:\mathrm{28}.\mathrm{5}}{\mathrm{sin}\:\mathrm{50}.\mathrm{5}} \\ $$$$\frac{{r}}{{q}}=\frac{\mathrm{sin}\:\frac{\mathrm{101}+\mathrm{98}}{\mathrm{2}}}{\mathrm{sin}\:\frac{\mathrm{32}+\mathrm{57}}{\mathrm{2}}}=\frac{\mathrm{sin}\:\mathrm{99}.\mathrm{5}}{\mathrm{sin}\:\mathrm{44}.\mathrm{5}} \\ $$$$\frac{{q}}{{p}}×\frac{{p}}{{r}}×\frac{{r}}{{q}}=\frac{\mathrm{sin}\:\mathrm{63}}{\mathrm{sin}\:\mathrm{52}}×\frac{\mathrm{sin}\:\mathrm{28}.\mathrm{5}}{\mathrm{sin}\:\mathrm{50}.\mathrm{5}}×\frac{\mathrm{sin}\:\mathrm{99}.\mathrm{5}}{\mathrm{sin}\:\mathrm{44}.\mathrm{5}} \\ $$$$\mathrm{1}\overset{?} {=}\frac{\mathrm{sin}\:\mathrm{63}\:}{\mathrm{sin}\:\mathrm{52}}\frac{\mathrm{sin}\:\mathrm{28}.\mathrm{5}\:}{\mathrm{sin}\:\mathrm{50}.\mathrm{5}}\frac{\mathrm{sin}\:\mathrm{99}.\mathrm{5}}{\mathrm{sin}\:\mathrm{44}.\mathrm{5}}\approx\mathrm{0}.\mathrm{98389}\neq\mathrm{1} \\ $$$$\Rightarrow{the}\:{three}\:{lines}\:{don}'{t}\:{intersect}\:{at} \\ $$$${the}\:{same}\:{point}! \\ $$
