Question-186784

Question Number 186784 by Rupesh123 last updated on 10/Feb/23

Answered by a.lgnaoui last updated on 11/Feb/23

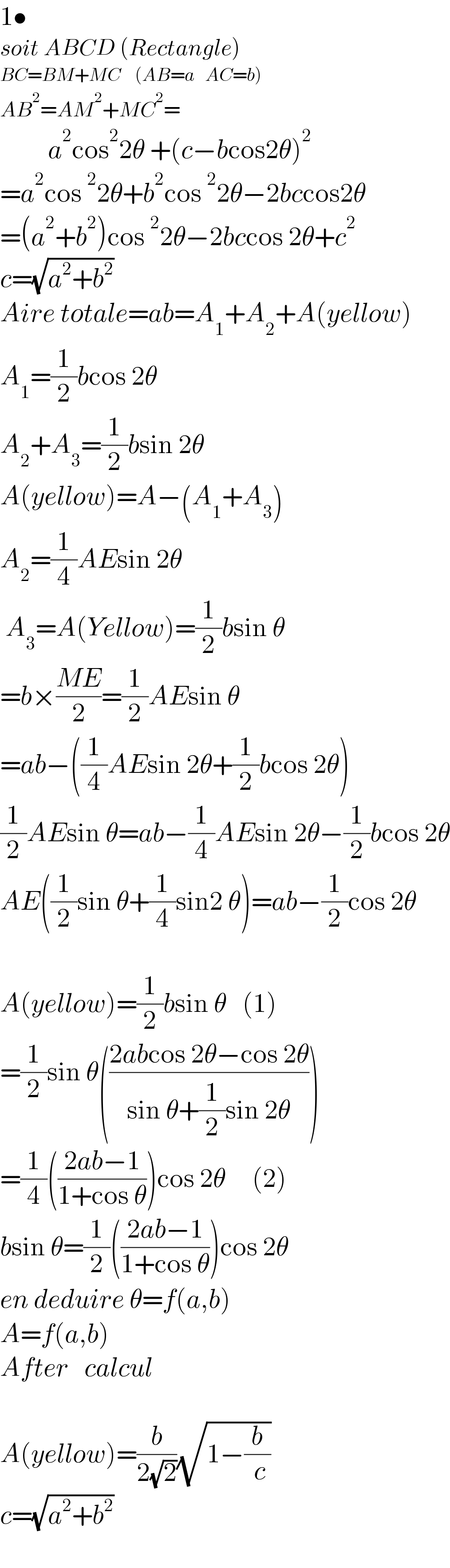
1• soit ABCD (Rectangle) BC=BM+MC (AB=a AC=b) AB^2 =AM^2 +MC^2 = a^2 cos^2 2θ +(c−bcos2θ)^2 =a^2 cos^2 2θ+b^2 cos^2 2θ−2bccos2θ =(a^2 +b^2 )cos^2 2θ−2bccos 2θ+c^2 c=(√(a^2 +b^2 )) Aire totale=ab=A_1 +A_2 +A(yellow) A_1 =(1/2)bcos 2θ A_2 +A_3 =(1/2)bsin 2θ A(yellow)=A−(A_1 +A_3 ) A_2 =(1/4)AEsin 2θ A_3 =A(Yellow)=(1/2)bsin θ =b×((ME)/2)=(1/2)AEsin θ =ab−((1/4)AEsin 2θ+(1/2)bcos 2θ) (1/2)AEsin θ=ab−(1/4)AEsin 2θ−(1/2)bcos 2θ AE((1/2)sin θ+(1/4)sin2 θ)=ab−(1/2)cos 2θ A(yellow)=(1/2)bsin θ (1) =(1/2)sin θ(((2abcos 2θ−cos 2θ)/(sin θ+(1/2)sin 2θ))) =(1/4)(((2ab−1)/(1+cos θ)))cos 2θ (2) bsin θ=(1/2)(((2ab−1)/(1+cos θ)))cos 2θ en deduire θ=f(a,b) A=f(a,b) After calcul A(yellow)=(b/(2(√2)))(√(1−(b/( c)))) c=(√(a^2 +b^2 ))

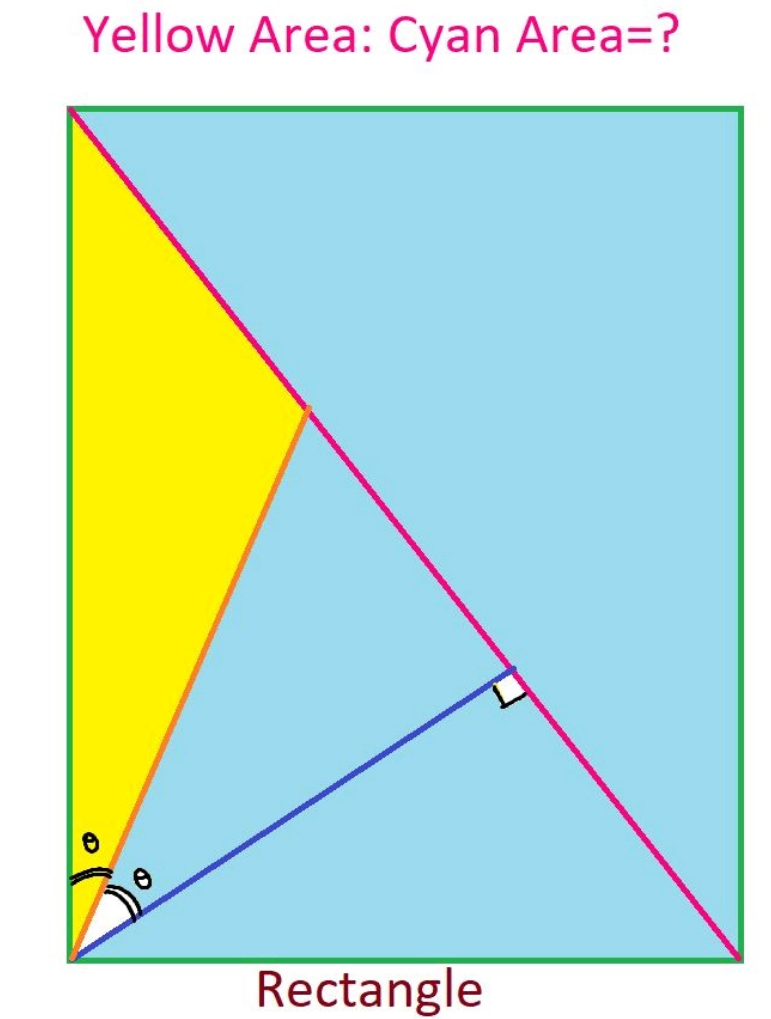
$$\mathrm{1}\bullet \\ $$$${soit}\:{ABCD}\:\left({Rectangle}\right) \\ $$$${BC}={BM}+{MC}\:\:\:\:\left({AB}={a}\:\:\:{AC}={b}\right) \\ $$$${AB}^{\mathrm{2}} ={AM}^{\mathrm{2}} +{MC}^{\mathrm{2}} = \\ $$$$\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{2}\theta\:+\left({c}−{b}\mathrm{cos2}\theta\right)^{\mathrm{2}} \\ $$$$={a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta+{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta−\mathrm{2}{bc}\mathrm{cos2}\theta \\ $$$$=\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta−\mathrm{2}{bc}\mathrm{cos}\:\mathrm{2}\theta+{c}^{\mathrm{2}} \\ $$$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${Aire}\:{totale}={ab}={A}_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}\left({yellow}\right) \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}{b}\mathrm{cos}\:\mathrm{2}\theta\:\: \\ $$$${A}_{\mathrm{2}} +{A}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}{b}\mathrm{sin}\:\mathrm{2}\theta \\ $$$${A}\left({yellow}\right)={A}−\left({A}_{\mathrm{1}} +{A}_{\mathrm{3}} \right) \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}{AE}\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\:{A}_{\mathrm{3}} ={A}\left({Yellow}\right)=\frac{\mathrm{1}}{\mathrm{2}}{b}\mathrm{sin}\:\theta \\ $$$$={b}×\frac{{ME}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{AE}\mathrm{sin}\:\theta \\ $$$$={ab}−\left(\frac{\mathrm{1}}{\mathrm{4}}{AE}\mathrm{sin}\:\mathrm{2}\theta+\frac{\mathrm{1}}{\mathrm{2}}{b}\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{AE}\mathrm{sin}\:\theta={ab}−\frac{\mathrm{1}}{\mathrm{4}}{AE}\mathrm{sin}\:\mathrm{2}\theta−\frac{\mathrm{1}}{\mathrm{2}}{b}\mathrm{cos}\:\mathrm{2}\theta \\ $$$${AE}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin2}\:\theta\right)={ab}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\:\:\:\:\:\:\:\: \\ $$$${A}\left({yellow}\right)=\frac{\mathrm{1}}{\mathrm{2}}{b}\mathrm{sin}\:\theta\:\:\:\left(\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\theta\left(\frac{\mathrm{2}{ab}\mathrm{cos}\:\mathrm{2}\theta−\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{2}{ab}−\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\theta}\right)\mathrm{cos}\:\mathrm{2}\theta\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$${b}\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}{ab}−\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\theta}\right)\mathrm{cos}\:\mathrm{2}\theta \\ $$$${en}\:{deduire}\:\theta={f}\left({a},{b}\right) \\ $$$${A}={f}\left({a},{b}\right) \\ $$$${After}\:\:\:{calcul} \\ $$$$ \\ $$$${A}\left({yellow}\right)=\frac{{b}}{\mathrm{2}\sqrt{\mathrm{2}}}\sqrt{\mathrm{1}−\frac{{b}}{\:{c}}} \\ $$$${c}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$ \\ $$

Commented by a.lgnaoui last updated on 11/Feb/23

Facebook Tweet Pin

Leave a Reply Cancel reply