Menu Close

Question-186868

Tinku Tara 0 Comments
Pin




Question Number 186868 by Mingma last updated on 11/Feb/23
Commented by Mingma last updated on 11/Feb/23
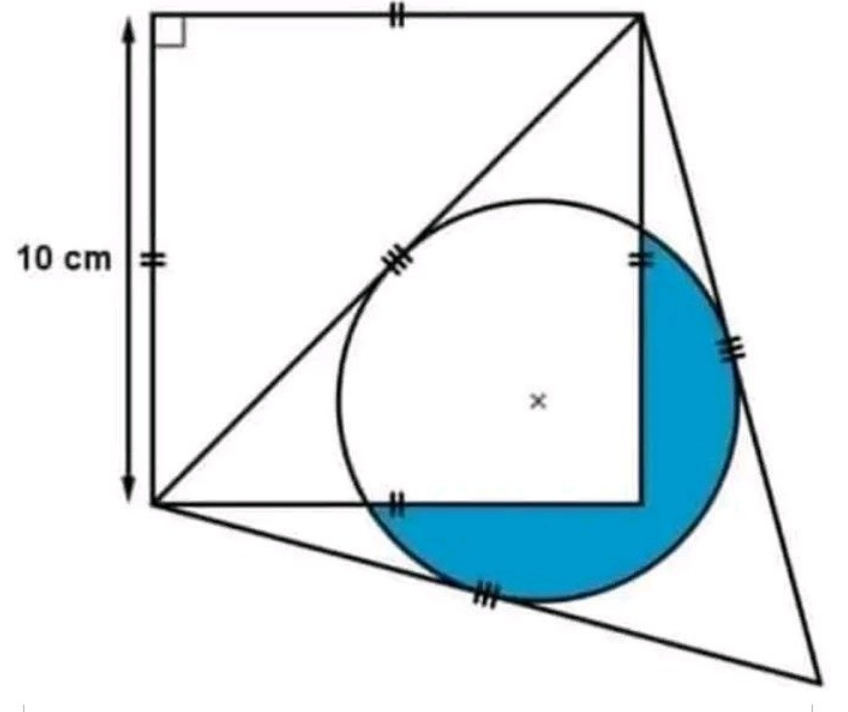
Shaded area =?
Answered by HeferH last updated on 11/Feb/23
Commented by Mingma last updated on 11/Feb/23
Good, but can you show your work
Commented by HeferH last updated on 12/Feb/23
Sorry sir, i was tired at the time but i have the solution in mind (getting the angle and then the area of the circular sector) Im probably gonna do it tomorrow
$${Sorry}\:{sir},\:{i}\:{was}\:{tired}\:{at}\:{the}\:{time}\:{but}\:{i}\:{have} \\ $$$$\:{the}\:{solution}\:{in}\:{mind}\:\left({getting}\:{the}\:{angle}\:{and}\right. \\ $$$$\left.\:{then}\:{the}\:{area}\:{of}\:{the}\:{circular}\:{sector}\right)\:{Im} \\ $$$$\:{probably}\:{gonna}\:{do}\:{it}\:{tomorrow}\: \\ $$
Commented by HeferH last updated on 13/Feb/23
Commented by HeferH last updated on 13/Feb/23
r: radius of the incircle AO^2 = x^2 + (AB−x)^2 r = ((5(√2))/( (√3))) = ((5(√6))/3) AO = ((10(√6))/3) ⇒ (((10(√6))/3))^2 = x^2 + (10 − x)^2 x = ((15±5(√3))/3) ; x < r ⇒ x = ((15 −5(√3))/3) sin α = (x/r) = (((15−5(√3))/3))∙ (3/(5(√6))) = ((3−(√3))/( (√6))) = (((√6)−(√2))/2) α = sin^(−1) ((((√6)−(√2))/2)) ≈ 31°⇒ β = 14° ⇒ 180°−2β = 180°−28° = 152° Area shaded = πr^2 −2Area(△)−Area(sector) Area (sector) = ((arc∙r)/2) = ((152°π)/(180°))(((5(√6))/3))^2 ∙(1/2) =((38π)/9)∙(5/3) = ((190π)/(27)) 2Area(△) = x(x + (√(r^2 −x^2 ))) = ((15−5(√3))/3)[((15−5(√3))/3) +((15−5(√3))/3) (√(((25∙6)/9) −(((15−5(√3))/3))^2 )) ] ≈ 11.8 ⇒Area shaded = πr^2 −2Area(△)−Area(sector) = ((260π)/(27)) −11.8 ≈ 18.452 Area shaded ≈ 18.452
$${r}:\:{radius}\:{of}\:{the}\:{incircle} \\ $$$$\:{AO}^{\mathrm{2}} \:\:=\:{x}^{\mathrm{2}} \:+\:\left({AB}−{x}\right)^{\mathrm{2}} \\ $$$$\:{r}\:=\:\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\:{AO}\:=\:\frac{\mathrm{10}\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\:\Rightarrow\:\left(\frac{\mathrm{10}\sqrt{\mathrm{6}}}{\mathrm{3}}\right)^{\mathrm{2}} \:=\:{x}^{\mathrm{2}} \:+\:\left(\mathrm{10}\:−\:{x}\right)^{\mathrm{2}} \\ $$$$\:{x}\:=\:\frac{\mathrm{15}\pm\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}\:;\:{x}\:<\:{r}\:\Rightarrow\:{x}\:=\:\frac{\mathrm{15}\:−\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\:\mathrm{sin}\:\alpha\:=\:\frac{{x}}{{r}}\:=\:\left(\frac{\mathrm{15}−\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\centerdot\:\frac{\mathrm{3}}{\mathrm{5}\sqrt{\mathrm{6}}}\:=\:\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{6}}}\:=\:\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\:\alpha\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\:\approx\:\mathrm{31}°\Rightarrow\: \\ $$$$\:\beta\:=\:\mathrm{14}°\:\Rightarrow \\ $$$$\:\mathrm{180}°−\mathrm{2}\beta\:=\:\mathrm{180}°−\mathrm{28}°\:=\:\mathrm{152}° \\ $$$$\:{Area}\:{shaded}\:\:=\:\pi{r}^{\mathrm{2}} −\mathrm{2}{Area}\left(\bigtriangleup\right)−{Area}\left({sector}\right) \\ $$$$\:{Area}\:\left({sector}\right)\:=\:\frac{{arc}\centerdot{r}}{\mathrm{2}}\:=\:\frac{\mathrm{152}°\pi}{\mathrm{180}°}\left(\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{3}}\right)^{\mathrm{2}} \centerdot\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:=\frac{\mathrm{38}\pi}{\mathrm{9}}\centerdot\frac{\mathrm{5}}{\mathrm{3}}\:=\:\frac{\mathrm{190}\pi}{\mathrm{27}} \\ $$$$\:\mathrm{2}{Area}\left(\bigtriangleup\right)\:=\:{x}\left({x}\:+\:\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }\right) \\ $$$$\:=\:\frac{\mathrm{15}−\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\frac{\mathrm{15}−\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}\:+\frac{\mathrm{15}−\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\sqrt{\frac{\mathrm{25}\centerdot\mathrm{6}}{\mathrm{9}}\:−\left(\frac{\mathrm{15}−\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)^{\mathrm{2}} \:}\:\right] \\ $$$$\:\approx\:\mathrm{11}.\mathrm{8}\: \\ $$$$\:\Rightarrow{Area}\:{shaded}\:\:=\:\pi{r}^{\mathrm{2}} −\mathrm{2}{Area}\left(\bigtriangleup\right)−{Area}\left({sector}\right) \\ $$$$\:=\:\frac{\mathrm{260}\pi}{\mathrm{27}}\:−\mathrm{11}.\mathrm{8}\:\approx\:\mathrm{18}.\mathrm{452} \\ $$$$\:{Area}\:{shaded}\:\approx\:\mathrm{18}.\mathrm{452} \\ $$
Answered by mr W last updated on 12/Feb/23
Commented by mr W last updated on 12/Feb/23
side length of equilateral triangle: s=10(√2) radius of circle: r=((s tan 30°)/2)=((5(√2))/( (√3)))=((5(√6))/3) OA=((10(√2))/2)−((5(√6))/3)=((5(3(√2)−(√6)))/3) sin α=((OA)/( (√2)×OB))=((5(3(√2)−(√6))×3)/( (√2)×3×5(√6)))=(((√6)−(√2))/( 2)) θ=π−(π/4)−α=((3π)/4)−sin^(−1) (((√6)−(√2))/2) sin θ=sin ((π/4)+α)=(1/( (√2)))(sin α+cos α) =(1/( (√2)))((((√6)−(√2))/2)+(√((√3)−1)))=(((√3)−1)/2)+(√(((√3)−1)/2)) shaded area: A_(shade) =2(((θr^2 )/2)−((r×OA sin θ)/2)) =θr^2 −r×OA sin θ =(((3π)/4)−sin^(−1) (((√6)−(√2))/2))×(((5(√6))/3))^2 −((5(√6))/3)×((5(3(√2)−(√6)))/3)×((((√3)−1)/2)+(√(((√3)−1)/2))) =((50)/3)(((3π)/4)−sin^(−1) (((√6)−(√2))/2))−((50((√3)−1))/3)×((((√3)−1)/2)+(√(((√3)−1)/2))) ≈18.354437
$${side}\:{length}\:{of}\:{equilateral}\:{triangle}: \\ $$$${s}=\mathrm{10}\sqrt{\mathrm{2}} \\ $$$${radius}\:{of}\:{circle}: \\ $$$${r}=\frac{{s}\:\mathrm{tan}\:\mathrm{30}°}{\mathrm{2}}=\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$${OA}=\frac{\mathrm{10}\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{3}}=\frac{\mathrm{5}\left(\mathrm{3}\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}\right)}{\mathrm{3}} \\ $$$$\mathrm{sin}\:\alpha=\frac{{OA}}{\:\sqrt{\mathrm{2}}×{OB}}=\frac{\mathrm{5}\left(\mathrm{3}\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}\right)×\mathrm{3}}{\:\sqrt{\mathrm{2}}×\mathrm{3}×\mathrm{5}\sqrt{\mathrm{6}}}=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\:\mathrm{2}} \\ $$$$\theta=\pi−\frac{\pi}{\mathrm{4}}−\alpha=\frac{\mathrm{3}\pi}{\mathrm{4}}−\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\theta=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\alpha\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{sin}\:\alpha+\mathrm{cos}\:\alpha\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}}+\sqrt{\sqrt{\mathrm{3}}−\mathrm{1}}\right)=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}} \\ $$$${shaded}\:{area}: \\ $$$${A}_{{shade}} =\mathrm{2}\left(\frac{\theta{r}^{\mathrm{2}} }{\mathrm{2}}−\frac{{r}×{OA}\:\mathrm{sin}\:\theta}{\mathrm{2}}\right) \\ $$$$\:\:\:=\theta{r}^{\mathrm{2}} −{r}×{OA}\:\mathrm{sin}\:\theta \\ $$$$\:\:\:=\left(\frac{\mathrm{3}\pi}{\mathrm{4}}−\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}}\right)×\left(\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{3}}×\frac{\mathrm{5}\left(\mathrm{3}\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}\right)}{\mathrm{3}}×\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}}\right) \\ $$$$\:\:\:=\frac{\mathrm{50}}{\mathrm{3}}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}−\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}}\right)−\frac{\mathrm{50}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{3}}×\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}}\right) \\ $$$$\:\:\:\approx\mathrm{18}.\mathrm{354437} \\ $$
Commented by Mingma last updated on 12/Feb/23
Excellent

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *