Question-186924

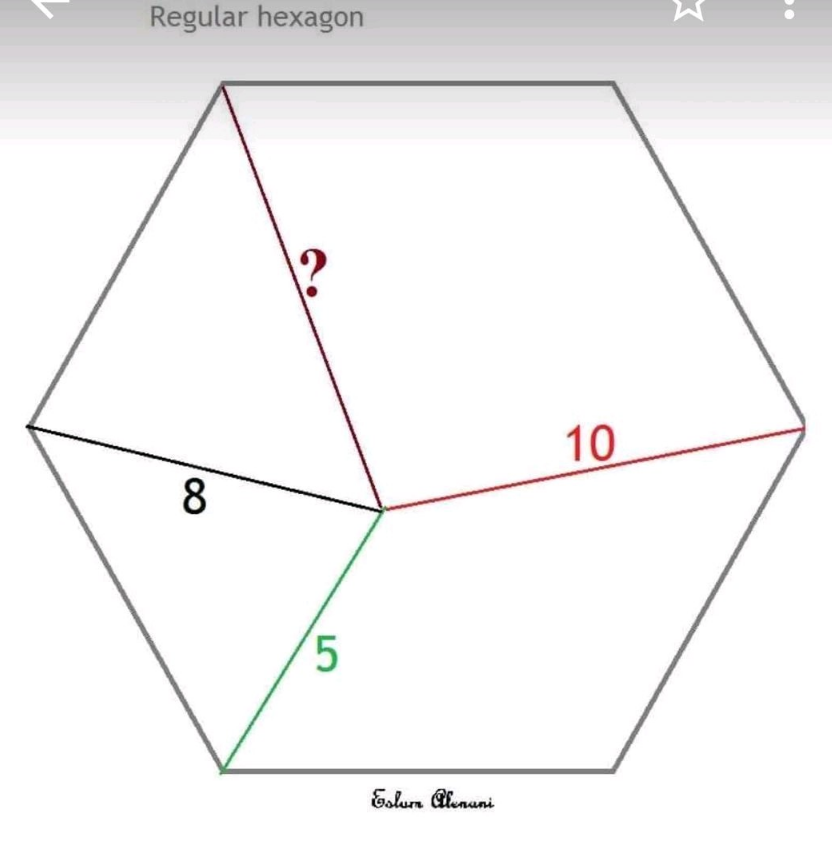
Question Number 186924 by Mingma last updated on 12/Feb/23

Answered by mr W last updated on 12/Feb/23

Commented by mr W last updated on 12/Feb/23

cos α=((s^2 +c^2 −a^2 )/(2sc)) cos γ=((4s^2 +c^2 −d^2 )/(4sc)) γ=(π/3)−α ((4s^2 +c^2 −d^2 )/(4sc))=(1/2){((s^2 +c^2 −a^2 )/(2sc))+((√(3[2(3c^2 −a^2 )s^2 −(c^2 −a^2 )^2 −s^4 ]))/(2sc))} 3s^2 −d^2 +a^2 =(√(3[2c^2 s^2 −s^4 −c^4 +2(s^2 +c^2 )a^2 −a^4 ])) 4a^4 −2(3c^2 +d^2 )a^2 +12s^4 −6(c^2 +d^2 )s^2 +3c^4 +d^4 =0 roots of this eqn. are a^2 and b^2 . a^2 +b^2 =((2(3c^2 +d^2 ))/4)=((3c^2 +d^2 )/2) that means there is following correlation between a,b,c,d: determinant (((2(a^2 +b^2 )=3c^2 +d^2 ))) a^2 b^2 =((12s^4 −6(c^2 +d^2 )s^2 +3c^4 +d^4 )/4) s^4 −(((c^2 +d^2 )s^2 )/2)+((3c^4 +d^4 −4a^2 b^2 )/(12))=0 s^2 =(1/4)[c^2 +d^2 +(√((16a^2 b^2 −(3c^2 −d^2 )^2 )/3))] ⇒s=(1/2)(√(c^2 +d^2 +(√((16a^2 b^2 −(3c^2 −d^2 )^2 )/3)))) in current case: a=5, c=8, d=10 5^2 +b^2 =((3×8^2 +10^2 )/2) ⇒b^2 =((3×8^2 +10^2 )/2)−5^2 =121 ⇒b=(√(121))=11

$$\mathrm{cos}\:\alpha=\frac{{s}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{sc}} \\ $$$$\mathrm{cos}\:\gamma=\frac{\mathrm{4}{s}^{\mathrm{2}} +{c}^{\mathrm{2}} −{d}^{\mathrm{2}} }{\mathrm{4}{sc}} \\ $$$$\gamma=\frac{\pi}{\mathrm{3}}−\alpha \\ $$$$\frac{\mathrm{4}{s}^{\mathrm{2}} +{c}^{\mathrm{2}} −{d}^{\mathrm{2}} }{\mathrm{4}{sc}}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{{s}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{sc}}+\frac{\sqrt{\mathrm{3}\left[\mathrm{2}\left(\mathrm{3}{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){s}^{\mathrm{2}} −\left({c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} −{s}^{\mathrm{4}} \right]}}{\mathrm{2}{sc}}\right\} \\ $$$$\mathrm{3}{s}^{\mathrm{2}} −{d}^{\mathrm{2}} +{a}^{\mathrm{2}} =\sqrt{\mathrm{3}\left[\mathrm{2}{c}^{\mathrm{2}} {s}^{\mathrm{2}} −{s}^{\mathrm{4}} −{c}^{\mathrm{4}} +\mathrm{2}\left({s}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){a}^{\mathrm{2}} −{a}^{\mathrm{4}} \right]} \\ $$$$\mathrm{4}{a}^{\mathrm{4}} −\mathrm{2}\left(\mathrm{3}{c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right){a}^{\mathrm{2}} +\mathrm{12}{s}^{\mathrm{4}} −\mathrm{6}\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right){s}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{4}} +{d}^{\mathrm{4}} =\mathrm{0} \\ $$$${roots}\:{of}\:{this}\:{eqn}.\:{are}\:{a}^{\mathrm{2}} \:{and}\:{b}^{\mathrm{2}} . \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{\mathrm{2}\left(\mathrm{3}{c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}{\mathrm{4}}=\frac{\mathrm{3}{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${that}\:{means}\:{there}\:{is}\:{following}\: \\ $$$${correlation}\:{between}\:{a},{b},{c},{d}: \\ $$$$\begin{array}{|c|}{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)=\mathrm{3}{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\\\hline\end{array} \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} =\frac{\mathrm{12}{s}^{\mathrm{4}} −\mathrm{6}\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right){s}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{4}} +{d}^{\mathrm{4}} }{\mathrm{4}} \\ $$$${s}^{\mathrm{4}} −\frac{\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right){s}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}{c}^{\mathrm{4}} +{d}^{\mathrm{4}} −\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\mathrm{12}}=\mathrm{0} \\ $$$${s}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left[{c}^{\mathrm{2}} +{d}^{\mathrm{2}} +\sqrt{\frac{\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\left(\mathrm{3}{c}^{\mathrm{2}} −{d}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{3}}}\right] \\ $$$$\Rightarrow{s}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} +\sqrt{\frac{\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\left(\mathrm{3}{c}^{\mathrm{2}} −{d}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{3}}}} \\ $$$${in}\:{current}\:{case}: \\ $$$${a}=\mathrm{5},\:{c}=\mathrm{8},\:{d}=\mathrm{10} \\ $$$$\mathrm{5}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{\mathrm{3}×\mathrm{8}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} =\frac{\mathrm{3}×\mathrm{8}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{5}^{\mathrm{2}} =\mathrm{121} \\ $$$$\Rightarrow{b}=\sqrt{\mathrm{121}}=\mathrm{11} \\ $$

Commented by Mingma last updated on 12/Feb/23

Excellent

Answered by nikif99 last updated on 12/Feb/23

In orthogonal yAx: Eq. of circle (A, r=5) at point K: K_x ^2 +K_y ^2 =5^2 (1) Eq. of (B, r=8) at K: (K_x −B_x )^2 +(K_y −B_y )^2 =8^2 ⇒ [K_x −(−(a/2))]^2 +(K_y −((a(√3))/2))^2 =64⇒ a(a+K_x −(√3)K_y )=39 (2) Eq. of (K, r=10) at E: (E_x −K_x )^2 +(E_y −K_y )^2 =10^2 ⇒ (a+(a/2)−K_x )^2 +(((a(√3))/2)−K_y )^2 =100 ⇒ a(3a−3K_x −(√3)K_y )=75 (3) (1)(2)(3) ⇒a=8.357297 K_x =3.101745, K_y =3.921629 CK=(√((K_x −C_x )^2 +(K_y −C_y )^2 )) ⇒CK=11

$$\underline{{In}\:{orthogonal}\:{yAx}:} \\ $$$${Eq}.\:{of}\:{circle}\:\left({A},\:{r}=\mathrm{5}\right)\:{at}\:{point}\:{K}:\:{K}_{{x}} ^{\mathrm{2}} +{K}_{{y}} ^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \:\left(\mathrm{1}\right) \\ $$$${Eq}.\:{of}\:\left({B},\:{r}=\mathrm{8}\right)\:{at}\:{K}:\:\left({K}_{{x}} −{B}_{{x}} \right)^{\mathrm{2}} +\left({K}_{{y}} −{B}_{{y}} \right)^{\mathrm{2}} =\mathrm{8}^{\mathrm{2}} \:\Rightarrow \\ $$$$\left[{K}_{{x}} −\left(−\frac{{a}}{\mathrm{2}}\right)\right]^{\mathrm{2}} +\left({K}_{{y}} −\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{64}\Rightarrow \\ $$$${a}\left({a}+{K}_{{x}} −\sqrt{\mathrm{3}}{K}_{{y}} \right)=\mathrm{39}\:\left(\mathrm{2}\right) \\ $$$${Eq}.\:{of}\:\left({K},\:{r}=\mathrm{10}\right)\:{at}\:{E}:\:\left({E}_{{x}} −{K}_{{x}} \right)^{\mathrm{2}} +\left({E}_{{y}} −{K}_{{y}} \right)^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} \:\Rightarrow \\ $$$$\left({a}+\frac{{a}}{\mathrm{2}}−{K}_{{x}} \right)^{\mathrm{2}} +\left(\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}−{K}_{{y}} \right)^{\mathrm{2}} =\mathrm{100}\:\Rightarrow \\ $$$${a}\left(\mathrm{3}{a}−\mathrm{3}{K}_{{x}} −\sqrt{\mathrm{3}}{K}_{{y}} \right)=\mathrm{75}\:\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{1}\right)\left(\mathrm{2}\right)\left(\mathrm{3}\right)\:\Rightarrow{a}=\mathrm{8}.\mathrm{357297} \\ $$$${K}_{{x}} =\mathrm{3}.\mathrm{101745},\:{K}_{{y}} =\mathrm{3}.\mathrm{921629} \\ $$$${CK}=\sqrt{\left({K}_{{x}} −{C}_{{x}} \right)^{\mathrm{2}} +\left({K}_{{y}} −{C}_{{y}} \right)^{\mathrm{2}} }\:\Rightarrow{CK}=\mathrm{11} \\ $$

Commented by nikif99 last updated on 12/Feb/23