Question Number 186966 by 073 last updated on 12/Feb/23

Commented by 073 last updated on 12/Feb/23

$$\mathrm{solution}\:? \\ $$
Commented by 073 last updated on 12/Feb/23

$$\mathrm{i}\:\mathrm{need}\:\mathrm{it}\:\mathrm{please}\: \\ $$$$\mathrm{solution}?? \\ $$
Answered by Rasheed.Sindhi last updated on 13/Feb/23
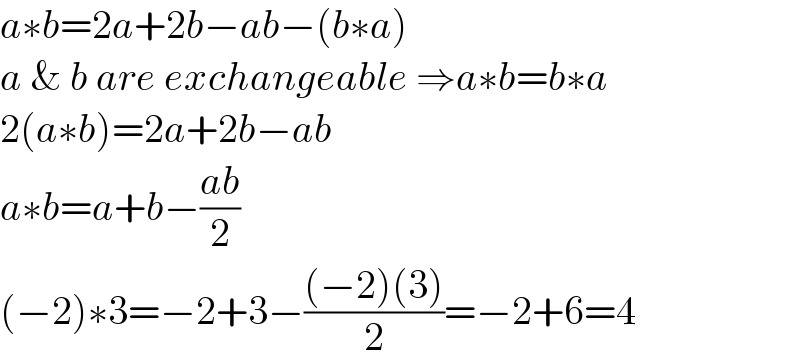
$${a}\ast{b}=\mathrm{2}{a}+\mathrm{2}{b}−{ab}−\left({b}\ast{a}\right) \\ $$$${a}\:\&\:{b}\:{are}\:{exchangeable}\:\Rightarrow{a}\ast{b}={b}\ast{a} \\ $$$$\mathrm{2}\left({a}\ast{b}\right)=\mathrm{2}{a}+\mathrm{2}{b}−{ab} \\ $$$${a}\ast{b}={a}+{b}−\frac{{ab}}{\mathrm{2}} \\ $$$$\left(−\mathrm{2}\right)\ast\mathrm{3}=−\mathrm{2}+\mathrm{3}−\frac{\left(−\mathrm{2}\right)\left(\mathrm{3}\right)}{\mathrm{2}}=−\mathrm{2}+\mathrm{6}=\mathrm{4} \\ $$
Commented by 073 last updated on 14/Feb/23

$$\mathrm{nice}\:\mathrm{solution} \\ $$$$\mathrm{thank}\:\mathrm{you}\: \\ $$
Commented by mr W last updated on 16/Feb/23
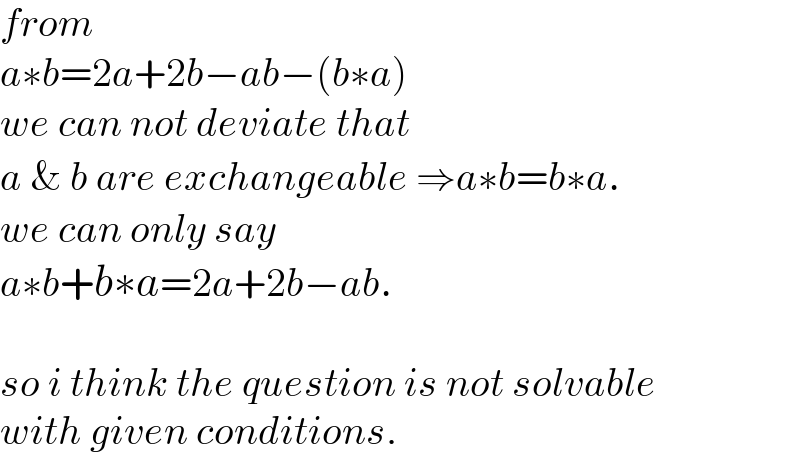
$${from} \\ $$$${a}\ast{b}=\mathrm{2}{a}+\mathrm{2}{b}−{ab}−\left({b}\ast{a}\right) \\ $$$${we}\:{can}\:{not}\:{deviate}\:{that} \\ $$$${a}\:\&\:{b}\:{are}\:{exchangeable}\:\Rightarrow{a}\ast{b}={b}\ast{a}. \\ $$$${we}\:{can}\:{only}\:{say} \\ $$$${a}\ast{b}+{b}\ast{a}=\mathrm{2}{a}+\mathrm{2}{b}−{ab}. \\ $$$$ \\ $$$${so}\:{i}\:{think}\:{the}\:{question}\:{is}\:{not}\:{solvable} \\ $$$${with}\:{given}\:{conditions}. \\ $$
Commented by Rasheed.Sindhi last updated on 16/Feb/23

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{lot}}\:\boldsymbol{\mathrm{sir}}! \\ $$
