Question Number 186998 by Mingma last updated on 12/Feb/23
Commented by a.lgnaoui last updated on 12/Feb/23

Answered by a.lgnaoui last updated on 12/Feb/23

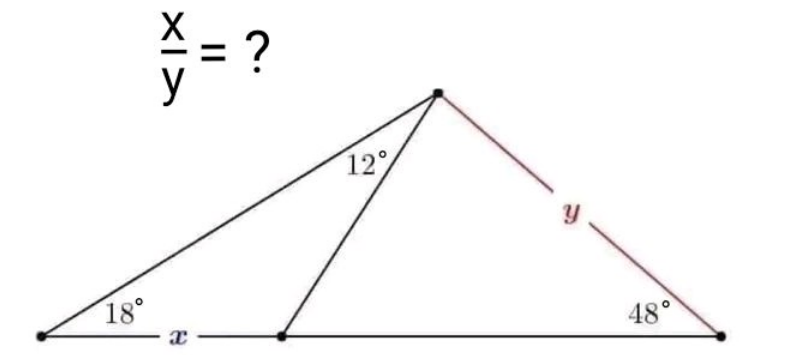
$$\bigtriangleup{ABC}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{12}}{{X}}=\frac{\mathrm{sin}\:\mathrm{18}}{{AD}}\:\:\:\left(\mathrm{1}\right) \\ $$$$\bigtriangleup{ABC}\:\:\:\: \\ $$$$\:\mathrm{12}+\mathrm{18}+\mathrm{48}+\measuredangle{CAD}=\mathrm{180} \\ $$$$\Rightarrow\measuredangle{CAD}=\mathrm{102}\:\Rightarrow\:\measuredangle{ADC}=\mathrm{180}−\mathrm{150}=\mathrm{30} \\ $$$$\bigtriangleup{ADC}\:\:\:\:\:\:\frac{\mathrm{sin}\:\mathrm{48}}{{AD}}\:=\frac{\mathrm{sin30}}{{Y}}\:\:\:\left(\mathrm{2}\right) \\ $$$$\:\:\left(\mathrm{1}\right)\Rightarrow\:\:\:\:\:\:\:\:\:{X}\mathrm{sin}\:\mathrm{18}={AD}\mathrm{sin}\:\mathrm{12} \\ $$$$\:\:\left(\mathrm{2}\right)\Rightarrow\:\:\:\:\:\:\:\:\:\:{Y}\mathrm{sin}\:\mathrm{48}={AD}\mathrm{sin}\:\mathrm{30} \\ $$$$\:\:\frac{\left(\mathrm{1}\right)}{\left(\mathrm{2}\right)}\Rightarrow\:\:\:\:\:\:\:\:\:\:\frac{{X}\mathrm{sin}\:\mathrm{18}}{{Y}\mathrm{sin}\:\mathrm{48}}=\frac{\mathrm{sin}\:\mathrm{12}}{\mathrm{sin}\:\mathrm{30}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{{X}}{{Y}}=\:\:\:\frac{\mathrm{sin}\:\mathrm{12}×\mathrm{sin}\:\mathrm{48}}{\mathrm{sin}\:\mathrm{30}×\mathrm{sin}\:\mathrm{18}}=\mathrm{1} \\ $$$$ \\ $$$${donc}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{X}={Y} \\ $$$$ \\ $$
Commented by Rupesh123 last updated on 13/Feb/23
Good
