Question-187301

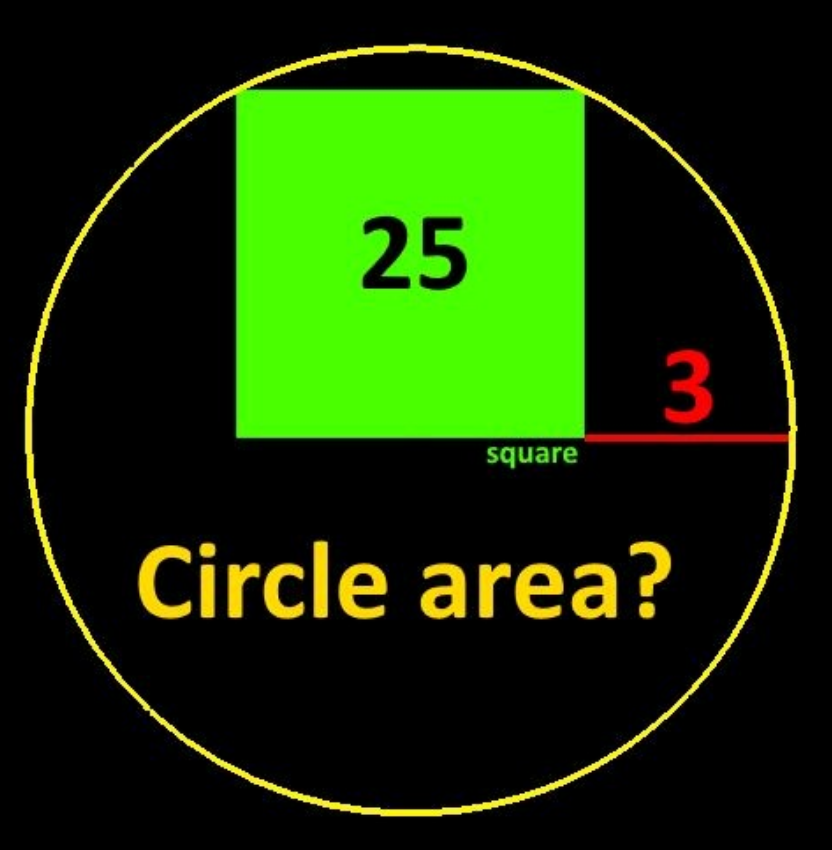
Question Number 187301 by Rupesh123 last updated on 15/Feb/23

Answered by HeferH last updated on 16/Feb/23

chord theorem: 5^2 = x(5 + 3) ((25)/8) = x ((25)/8) + 8 = 2r ((225)/(16)) = r A ≠ ((225^2 )/(16^2 ))π = ((11025π)/(256)) (i assumed that the line was diameter which is false)

$$\:{chord}\:{theorem}: \\ $$$$\mathrm{5}^{\mathrm{2}} \:=\:{x}\left(\mathrm{5}\:+\:\mathrm{3}\right) \\ $$$$\:\frac{\mathrm{25}}{\mathrm{8}}\:=\:{x} \\ $$$$\:\frac{\mathrm{25}}{\mathrm{8}}\:+\:\mathrm{8}\:=\:\mathrm{2}{r} \\ $$$$\:\frac{\mathrm{225}}{\mathrm{16}}\:=\:{r} \\ $$$$\:{A}\:\neq\:\:\frac{\mathrm{225}^{\mathrm{2}} }{\mathrm{16}^{\mathrm{2}} }\pi\:\:=\:\frac{\mathrm{11025}\pi}{\mathrm{256}}\:\left({i}\:{assumed}\right. \\ $$$$\left.\:{that}\:{the}\:{line}\:{was}\:{diameter}\:{which}\:{is}\:{false}\right) \\ $$$$\: \\ $$

Commented by Rupesh123 last updated on 15/Feb/23

Good!

Commented by Rupesh123 last updated on 15/Feb/23

Please note that it doesn't say the bottom of the square is coincident with the diameter

Commented by HeferH last updated on 15/Feb/23

$${Yes}\:{sir},\:{you}\:{are}\:{right},\:{im}\:{going}\:{to}\:{correct}\:{it}\: \\ $$

Commented by HeferH last updated on 15/Feb/23

Commented by HeferH last updated on 15/Feb/23

b(5 + 3) = 5a 3(b + 5) = 5a 8b = 3b + 15 b = 3 ⇒ a = ((24)/5) r^2 = ((25 + (5 + a)^2 )/4) = ((25 + ((2401)/(25)))/4) = ((625+2401)/(100)) = ((3026)/(100)) = ((1513)/(50)) A = ((1513π)/(50))

$${b}\left(\mathrm{5}\:+\:\mathrm{3}\right)\:=\:\mathrm{5}{a} \\ $$$$\mathrm{3}\left({b}\:+\:\mathrm{5}\right)\:=\:\mathrm{5}{a} \\ $$$$\:\mathrm{8}{b}\:=\:\mathrm{3}{b}\:+\:\mathrm{15} \\ $$$$\:{b}\:=\:\mathrm{3} \\ $$$$\:\Rightarrow\:{a}\:=\:\frac{\mathrm{24}}{\mathrm{5}} \\ $$$$\:{r}^{\mathrm{2}} \:=\:\frac{\mathrm{25}\:+\:\left(\mathrm{5}\:+\:{a}\right)^{\mathrm{2}} }{\mathrm{4}}\:=\:\frac{\mathrm{25}\:+\:\frac{\mathrm{2401}}{\mathrm{25}}}{\mathrm{4}}\:=\:\frac{\mathrm{625}+\mathrm{2401}}{\mathrm{100}} \\ $$$$\:=\:\frac{\mathrm{3026}}{\mathrm{100}}\:=\:\frac{\mathrm{1513}}{\mathrm{50}}\: \\ $$$$\:{A}\:=\:\frac{\mathrm{1513}\pi}{\mathrm{50}} \\ $$$$\: \\ $$

Commented by Rupesh123 last updated on 16/Feb/23

Excellent

Answered by mr W last updated on 15/Feb/23

Commented by mr W last updated on 15/Feb/23

AB=(√(3^2 +5^2 ))=(√(34)) BC=(√(5^2 +(5+3)^2 ))=(√(89)) sin θ=(5/( (√(34)))) 2R=((BC)/(sin θ))=(((√(89))×(√(34)))/5)=((√(3026))/5) R=((√(3026))/(10)) area of circle =πR^2 =((3026π)/(100))=((1513π)/(50))

$${AB}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }=\sqrt{\mathrm{34}} \\ $$$${BC}=\sqrt{\mathrm{5}^{\mathrm{2}} +\left(\mathrm{5}+\mathrm{3}\right)^{\mathrm{2}} }=\sqrt{\mathrm{89}} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{5}}{\:\sqrt{\mathrm{34}}} \\ $$$$\mathrm{2}{R}=\frac{{BC}}{\mathrm{sin}\:\theta}=\frac{\sqrt{\mathrm{89}}×\sqrt{\mathrm{34}}}{\mathrm{5}}=\frac{\sqrt{\mathrm{3026}}}{\mathrm{5}} \\ $$$${R}=\frac{\sqrt{\mathrm{3026}}}{\mathrm{10}} \\ $$$${area}\:{of}\:{circle}\:=\pi{R}^{\mathrm{2}} =\frac{\mathrm{3026}\pi}{\mathrm{100}}=\frac{\mathrm{1513}\pi}{\mathrm{50}} \\ $$

Commented by Rupesh123 last updated on 15/Feb/23

Excellent

Facebook Tweet Pin

Leave a Reply Cancel reply