Question Number 187452 by Rupesh123 last updated on 17/Feb/23

Answered by mr W last updated on 17/Feb/23
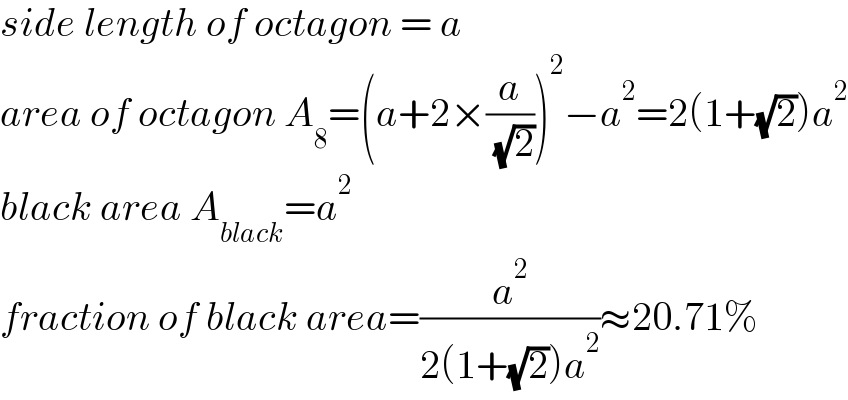
$${side}\:{length}\:{of}\:{octagon}\:=\:{a} \\ $$$${area}\:{of}\:{octagon}\:{A}_{\mathrm{8}} =\left({a}+\mathrm{2}×\frac{{a}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){a}^{\mathrm{2}} \\ $$$${black}\:{area}\:{A}_{{black}} ={a}^{\mathrm{2}} \\ $$$${fraction}\:{of}\:{black}\:{area}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){a}^{\mathrm{2}} }\approx\mathrm{20}.\mathrm{71\%} \\ $$
Commented by Rupesh123 last updated on 17/Feb/23
Good
Answered by HeferH last updated on 17/Feb/23

$${Total}\:{area}\:=\:\frac{{P}\centerdot{a}}{\mathrm{2}} \\ $$$$\:{a}:\:{apothem} \\ $$$$\:{P}:\:{perimeter} \\ $$$$\:{let}\:{x}\:{be}\:{the}\:{side}\:{of}\:{the}\:{octagon} \\ $$$$\:{Total}\:{area}\:=\:\mathrm{8}{x}\:\centerdot\:\left(\frac{{x}\:+\:{x}\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\:\centerdot\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:{area}\:{shaded}\:=\:{x}^{\mathrm{2}} \\ $$$$\frac{{Total}\:{area}}{{area}\:{shaded}}\:=\:\:\frac{{x}^{\mathrm{2}} }{\frac{\mathrm{8}{x}^{\mathrm{2}} \left(\mathrm{1}\:+\sqrt{\mathrm{2}}\right)}{\mathrm{4}}}\:=\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}=\:\frac{\mathrm{1}}{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}\: \\ $$
Commented by Rupesh123 last updated on 17/Feb/23
Excellent!
