Question-187476

Question Number 187476 by mnjuly1970 last updated on 17/Feb/23

Answered by anurup last updated on 18/Feb/23

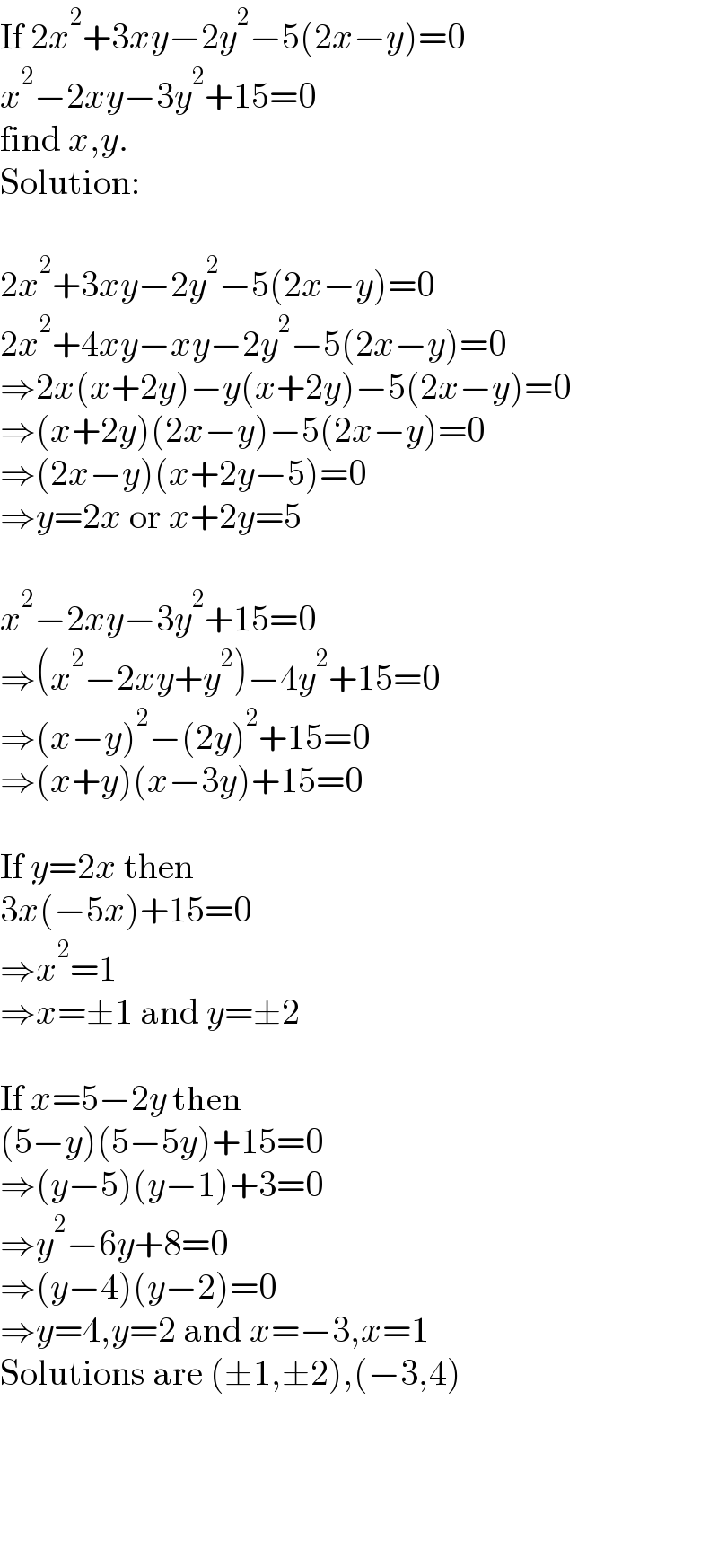
If 2x^2 +3xy−2y^2 −5(2x−y)=0 x^2 −2xy−3y^2 +15=0 find x,y. Solution: 2x^2 +3xy−2y^2 −5(2x−y)=0 2x^2 +4xy−xy−2y^2 −5(2x−y)=0 ⇒2x(x+2y)−y(x+2y)−5(2x−y)=0 ⇒(x+2y)(2x−y)−5(2x−y)=0 ⇒(2x−y)(x+2y−5)=0 ⇒y=2x or x+2y=5 x^2 −2xy−3y^2 +15=0 ⇒(x^2 −2xy+y^2 )−4y^2 +15=0 ⇒(x−y)^2 −(2y)^2 +15=0 ⇒(x+y)(x−3y)+15=0 If y=2x then 3x(−5x)+15=0 ⇒x^2 =1 ⇒x=±1 and y=±2 If x=5−2y then (5−y)(5−5y)+15=0 ⇒(y−5)(y−1)+3=0 ⇒y^2 −6y+8=0 ⇒(y−4)(y−2)=0 ⇒y=4,y=2 and x=−3,x=1 Solutions are (±1,±2),(−3,4)

$$\mathrm{If}\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{xy}−\mathrm{2}{y}^{\mathrm{2}} −\mathrm{5}\left(\mathrm{2}{x}−{y}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{xy}−\mathrm{3}{y}^{\mathrm{2}} +\mathrm{15}=\mathrm{0} \\ $$$$\mathrm{find}\:{x},{y}. \\ $$$$\mathrm{Solution}:\: \\ $$$$ \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{xy}−\mathrm{2}{y}^{\mathrm{2}} −\mathrm{5}\left(\mathrm{2}{x}−{y}\right)=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{xy}−{xy}−\mathrm{2}{y}^{\mathrm{2}} −\mathrm{5}\left(\mathrm{2}{x}−{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{x}\left({x}+\mathrm{2}{y}\right)−{y}\left({x}+\mathrm{2}{y}\right)−\mathrm{5}\left(\mathrm{2}{x}−{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}+\mathrm{2}{y}\right)\left(\mathrm{2}{x}−{y}\right)−\mathrm{5}\left(\mathrm{2}{x}−{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{x}−{y}\right)\left({x}+\mathrm{2}{y}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow{y}=\mathrm{2}{x}\:\mathrm{or}\:{x}+\mathrm{2}{y}=\mathrm{5} \\ $$$$ \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{xy}−\mathrm{3}{y}^{\mathrm{2}} +\mathrm{15}=\mathrm{0} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} −\mathrm{2}{xy}+{y}^{\mathrm{2}} \right)−\mathrm{4}{y}^{\mathrm{2}} +\mathrm{15}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−{y}\right)^{\mathrm{2}} −\left(\mathrm{2}{y}\right)^{\mathrm{2}} +\mathrm{15}=\mathrm{0} \\ $$$$\Rightarrow\left({x}+{y}\right)\left({x}−\mathrm{3}{y}\right)+\mathrm{15}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{If}\:{y}=\mathrm{2}{x}\:\mathrm{then}\: \\ $$$$\mathrm{3}{x}\left(−\mathrm{5}{x}\right)+\mathrm{15}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{x}=\pm\mathrm{1}\:\mathrm{and}\:{y}=\pm\mathrm{2} \\ $$$$ \\ $$$$\mathrm{If}\:{x}=\mathrm{5}−\mathrm{2}{y}\:\mathrm{then}\: \\ $$$$\left(\mathrm{5}−{y}\right)\left(\mathrm{5}−\mathrm{5}{y}\right)+\mathrm{15}=\mathrm{0} \\ $$$$\Rightarrow\left({y}−\mathrm{5}\right)\left({y}−\mathrm{1}\right)+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\mathrm{6}{y}+\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow\left({y}−\mathrm{4}\right)\left({y}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow{y}=\mathrm{4},{y}=\mathrm{2}\:\mathrm{and}\:{x}=−\mathrm{3},{x}=\mathrm{1} \\ $$$$\mathrm{Solutions}\:\mathrm{are}\:\left(\pm\mathrm{1},\pm\mathrm{2}\right),\left(−\mathrm{3},\mathrm{4}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by anurup last updated on 17/Feb/23

$$\mathrm{it}'\mathrm{s}\:\mathrm{quite}\:\mathrm{easy} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply