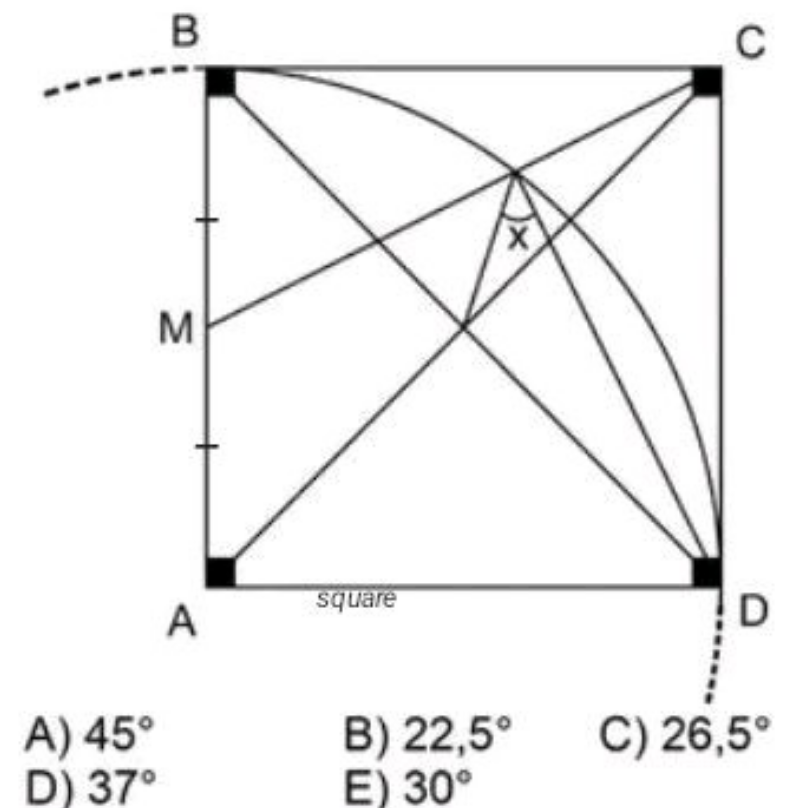
Question Number 187810 by Rupesh123 last updated on 22/Feb/23
Commented by a.lgnaoui last updated on 23/Feb/23

$$\left.\mathrm{E}\right)\mathrm{30} \\ $$
Commented by mr W last updated on 23/Feb/23

$${wrong}! \\ $$
Answered by mr W last updated on 23/Feb/23

Commented by mr W last updated on 23/Feb/23

$${say}\:{R}=\mathrm{2} \\ $$$${ED}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}}×\mathrm{1}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}} \\ $$$${FD}=\sqrt{\mathrm{2}} \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\alpha=\frac{\pi}{\mathrm{4}}−\beta \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{cos}\:\beta−\mathrm{sin}\:\alpha\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}} \\ $$$$\frac{\mathrm{sin}\:\left({x}+\alpha\right)}{\mathrm{sin}\:{x}}=\frac{{ED}}{{FD}}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{10}}} \\ $$$$\mathrm{cos}\:\alpha+\frac{\mathrm{sin}\:\alpha}{\mathrm{tan}\:{x}}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{10}}} \\ $$$$\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}+\frac{\mathrm{1}}{\mathrm{tan}\:{x}\sqrt{\mathrm{10}}}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{10}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:{x}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{tan}\:{x}=\mathrm{1}\:\Rightarrow{x}=\mathrm{45}°\:\checkmark \\ $$
Commented by Rupesh123 last updated on 23/Feb/23
Perfect ��
