Question Number 187827 by Rupesh123 last updated on 22/Feb/23
Answered by cortano12 last updated on 23/Feb/23

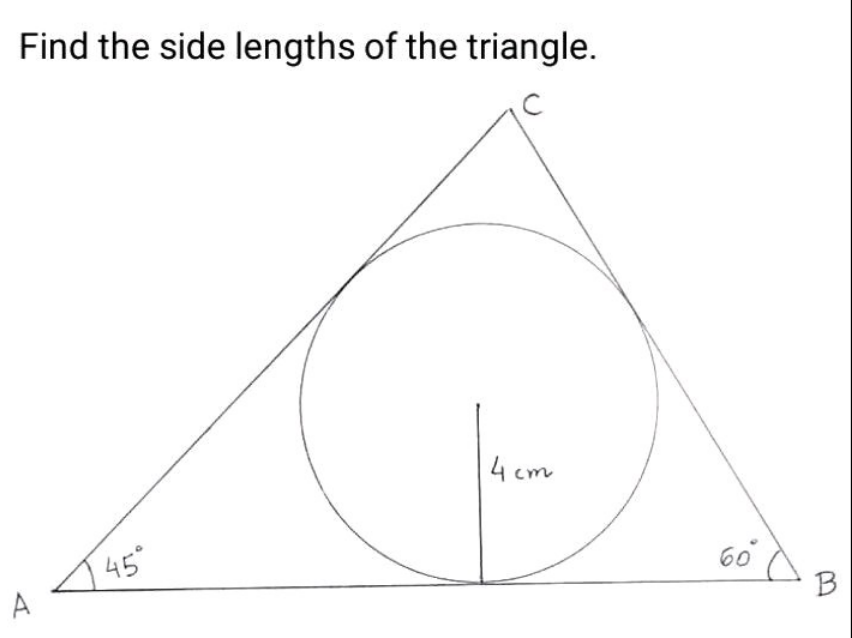
$$\left(\mathrm{1}\right)\mathrm{tan}\:\mathrm{30}°=\frac{\mathrm{4}}{\mathrm{a}}\Rightarrow\mathrm{a}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{tan}\:\mathrm{22},\mathrm{5}^{\mathrm{o}} \:=\frac{\mathrm{4}}{\mathrm{b}}\:;\:\mathrm{tan}\:\mathrm{45}°=\frac{\mathrm{2tan}\:\mathrm{22},\mathrm{5}^{\mathrm{o}} }{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{22},\mathrm{5}^{\mathrm{o}} } \\ $$$$\Rightarrow\mathrm{tan}\:^{\mathrm{2}} \mathrm{22},\mathrm{5}^{\mathrm{o}} +\mathrm{2tan}\:\mathrm{22},\mathrm{5}^{\mathrm{o}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{22},\mathrm{5}^{\mathrm{o}} =\frac{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}}=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{b}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}=\mathrm{4}\sqrt{\mathrm{2}}+\mathrm{4} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{tan}\:\mathrm{37},\mathrm{5}^{\mathrm{o}} =\frac{\mathrm{4}}{\mathrm{c}}\:;\:\mathrm{tan}\:\mathrm{75}^{\mathrm{o}} =\frac{\mathrm{2tan}\:\mathrm{37},\mathrm{5}^{\mathrm{o}} }{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{37},\mathrm{5}^{\mathrm{o}} } \\ $$$$\Rightarrow\mathrm{2}+\sqrt{\mathrm{3}}=\frac{\mathrm{2tan}\:\mathrm{37},\mathrm{5}^{\mathrm{o}} }{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{37},\mathrm{5}^{\mathrm{o}} } \\ $$$$\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{tan}\:^{\mathrm{2}} \mathrm{37},\mathrm{5}^{\mathrm{o}} +\mathrm{2tan}\:\mathrm{37},\mathrm{5}^{\mathrm{o}} −\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{37},\mathrm{5}^{\mathrm{o}} =\frac{−\mathrm{2}+\sqrt{\mathrm{11}+\mathrm{2}\sqrt{\mathrm{12}}}}{\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{37},\mathrm{5}^{\mathrm{o}} =\frac{\mathrm{5}\sqrt{\mathrm{3}}−\mathrm{8}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{c}=\frac{\mathrm{8}}{\:\mathrm{5}\sqrt{\mathrm{3}}−\mathrm{2}}=\frac{\mathrm{8}}{\mathrm{71}}\left(\mathrm{5}\sqrt{\mathrm{3}}+\mathrm{2}\right) \\ $$$$\therefore\:\mathrm{sides}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle} \\ $$$$\:=\begin{cases}{\mathrm{a}+\mathrm{b}=\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{4}\sqrt{\mathrm{2}}+\mathrm{4}}\\{\mathrm{a}+\mathrm{c}=\mathrm{4}\sqrt{\mathrm{3}}+\frac{\mathrm{16}+\mathrm{40}\sqrt{\mathrm{3}}}{\mathrm{71}}=\frac{\mathrm{324}\sqrt{\mathrm{3}}+\mathrm{16}}{\mathrm{71}}}\\{\mathrm{b}+\mathrm{c}=\mathrm{4}\sqrt{\mathrm{2}}+\mathrm{4}+\frac{\mathrm{40}\sqrt{\mathrm{3}}+\mathrm{16}}{\mathrm{71}}=\frac{\mathrm{300}+\mathrm{284}\sqrt{\mathrm{2}}+\mathrm{40}\sqrt{\mathrm{3}}}{\mathrm{71}}}\end{cases}\:\:\: \\ $$$$ \\ $$
Commented by Rupesh123 last updated on 22/Feb/23
Very nice work!
Answered by nikif99 last updated on 22/Feb/23

$${Let}\:{incenter}:\:{I}.\:{Let}\:{ID}\:{radius}=\mathrm{4}\:{cm} \\ $$$$\measuredangle{C}=\mathrm{75}° \\ $$$${AD}=\frac{{ID}}{\mathrm{tan}\:\mathrm{22}.\mathrm{5}}=\mathrm{4}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$${BD}=\frac{{ID}}{\mathrm{tan}\:\mathrm{30}}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$$${AB}=\mathrm{4}\left(\mathrm{1}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)\:{cm}\:\left(\mathrm{1}\right) \\ $$$$\frac{{AC}}{\mathrm{sin}\:\mathrm{60}}=\frac{{AB}}{\mathrm{sin}\:\mathrm{75}}=\frac{{BC}}{\mathrm{sin}\:\mathrm{45}}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\left(\mathrm{2}\right)\:\Rightarrow{AC}=\mathrm{4}\left(\mathrm{3}−\sqrt{\mathrm{3}}+\sqrt{\mathrm{6}}\right)\:{cm} \\ $$$${BC}=\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}\right)\:{cm} \\ $$
