Menu Close

Question-187891

Tinku Tara 0 Comments
Pin




Question Number 187891 by Rupesh123 last updated on 23/Feb/23
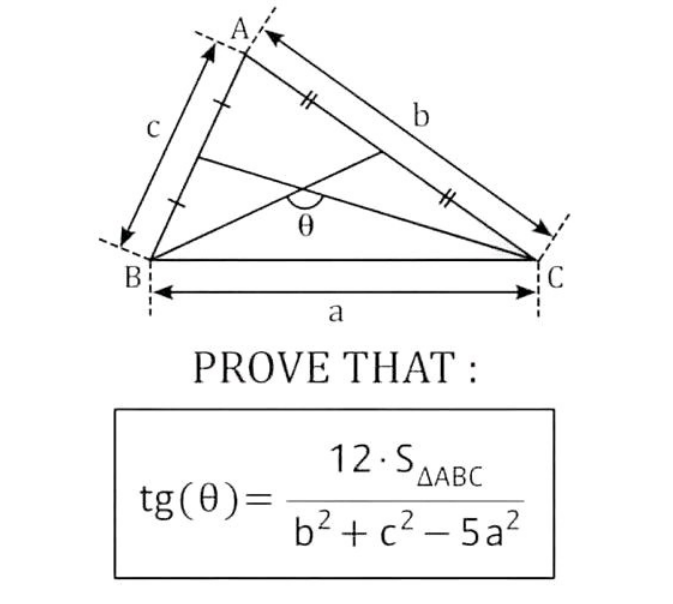
Answered by mr W last updated on 24/Feb/23
Commented by mr W last updated on 25/Feb/23
Δ=area of ΔABC ((sin (β+C))/(sin β))=(a/(b/2))=((2a)/b) cos C+((sin C)/(tan β))=((2a)/b) ((a^2 +b^2 −c^2 )/(2ab))+((2Δ)/(ab tan β))=((2a)/b) tan β=((4Δ)/(3a^2 −b^2 +c^2 )) similarly tan γ=((4Δ)/(3a^2 −c^2 +b^2 )) θ=π−(β+γ) tan θ=−tan (β+γ)=−((tan β+tan γ)/(1−tan β tan γ)) =((((4Δ)/(3a^2 −b^2 +c^2 ))+((4Δ)/(3a^2 −c^2 +b^2 )))/(((4Δ)/(3a^2 −b^2 +c^2 ))×((4Δ)/(3a^2 −c^2 +b^2 ))−1)) =((6a^2 )/(16Δ^2 −(3a^2 −b^2 +c^2 )(3a^2 −c^2 +b^2 )))×4Δ =((24a^2 Δ)/(16Δ^2 −(3a^2 )^2 +(b^2 −c^2 )^2 )) =((24a^2 Δ)/(2(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^4 +b^4 +c^4 )−9a^4 +b^4 +c^4 −2b^2 c^2 )) =((12a^2 Δ)/(a^2 b^2 +c^2 a^2 −5a^4 )) =((12Δ)/(b^2 +c^2 −5a^2 )) ✓
$$\Delta={area}\:{of}\:\Delta{ABC} \\ $$$$\frac{\mathrm{sin}\:\left(\beta+{C}\right)}{\mathrm{sin}\:\beta}=\frac{{a}}{\frac{{b}}{\mathrm{2}}}=\frac{\mathrm{2}{a}}{{b}} \\ $$$$\mathrm{cos}\:{C}+\frac{\mathrm{sin}\:{C}}{\mathrm{tan}\:\beta}=\frac{\mathrm{2}{a}}{{b}} \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}}+\frac{\mathrm{2}\Delta}{{ab}\:\mathrm{tan}\:\beta}=\frac{\mathrm{2}{a}}{{b}} \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{4}\Delta}{\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$${similarly} \\ $$$$\mathrm{tan}\:\gamma=\frac{\mathrm{4}\Delta}{\mathrm{3}{a}^{\mathrm{2}} −{c}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\theta=\pi−\left(\beta+\gamma\right) \\ $$$$\mathrm{tan}\:\theta=−\mathrm{tan}\:\left(\beta+\gamma\right)=−\frac{\mathrm{tan}\:\beta+\mathrm{tan}\:\gamma}{\mathrm{1}−\mathrm{tan}\:\beta\:\mathrm{tan}\:\gamma} \\ $$$$\:\:=\frac{\frac{\mathrm{4}\Delta}{\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }+\frac{\mathrm{4}\Delta}{\mathrm{3}{a}^{\mathrm{2}} −{c}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\frac{\mathrm{4}\Delta}{\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }×\frac{\mathrm{4}\Delta}{\mathrm{3}{a}^{\mathrm{2}} −{c}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\mathrm{1}} \\ $$$$\:\:=\frac{\mathrm{6}{a}^{\mathrm{2}} }{\mathrm{16}\Delta^{\mathrm{2}} −\left(\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left(\mathrm{3}{a}^{\mathrm{2}} −{c}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}×\mathrm{4}\Delta \\ $$$$\:\:=\frac{\mathrm{24}{a}^{\mathrm{2}} \Delta}{\mathrm{16}\Delta^{\mathrm{2}} −\left(\mathrm{3}{a}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:=\frac{\mathrm{24}{a}^{\mathrm{2}} \Delta}{\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)−\mathrm{9}{a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} −\mathrm{2}{b}^{\mathrm{2}} {c}^{\mathrm{2}} } \\ $$$$\:\:=\frac{\mathrm{12}{a}^{\mathrm{2}} \Delta}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} −\mathrm{5}{a}^{\mathrm{4}} } \\ $$$$\:\:=\frac{\mathrm{12}\Delta}{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{5}{a}^{\mathrm{2}} }\:\checkmark \\ $$
Commented by Rupesh123 last updated on 26/Feb/23
Excellent, sir!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *