Question Number 187901 by Rupesh123 last updated on 23/Feb/23
Commented by Rupesh123 last updated on 23/Feb/23
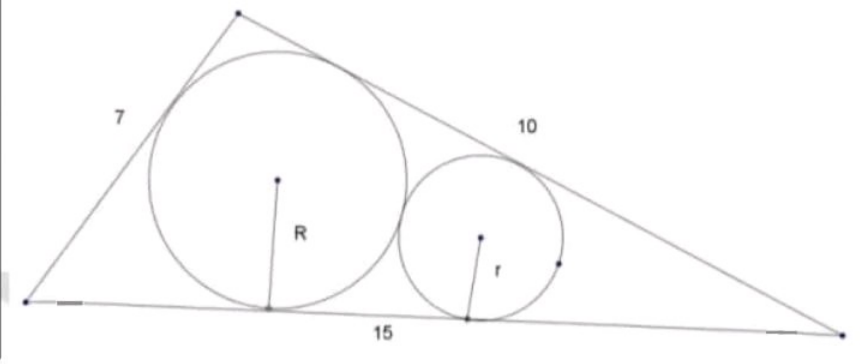
Find R and r
Commented by BaliramKumar last updated on 23/Feb/23

$${R}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{4}} \\ $$
Answered by mr W last updated on 23/Feb/23

$${s}=\frac{\mathrm{7}+\mathrm{10}+\mathrm{15}}{\mathrm{2}}=\mathrm{16} \\ $$$$\Delta=\sqrt{\mathrm{16}×\mathrm{9}×\mathrm{6}×\mathrm{1}}=\mathrm{12}\sqrt{\mathrm{6}} \\ $$$${R}=\frac{\Delta}{{s}}=\frac{\mathrm{12}\sqrt{\mathrm{6}}}{\mathrm{16}}=\frac{\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:{C}=\frac{\mathrm{15}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }{\mathrm{2}×\mathrm{15}×\mathrm{10}}=\frac{\mathrm{23}}{\mathrm{25}} \\ $$$$\frac{{R}−{r}}{{R}+{r}}=\mathrm{sin}\:\frac{{C}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:{C}}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}{R}}{\mathrm{3}}=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\:\checkmark \\ $$
Commented by Rupesh123 last updated on 23/Feb/23
Very nice solution!
Answered by HeferH last updated on 23/Feb/23

$$\:{A}\:=\:{s}\centerdot{I};\:{I}\:=\:{R} \\ $$$$\:{s}\:=\:\frac{\mathrm{7}+\mathrm{10}+\mathrm{15}}{\mathrm{2}}\:=\:\mathrm{16} \\ $$$$\:{R}\:=\:\frac{{A}}{{s}}\:=\:\frac{\sqrt{\mathrm{16}\left(\mathrm{16}−\mathrm{10}\right)\left(\mathrm{16}−\mathrm{15}\right)\left(\mathrm{16}−\mathrm{7}\right)}}{\mathrm{16}}\:=\:\frac{\sqrt{\mathrm{16}\centerdot\mathrm{6}\centerdot\mathrm{9}}}{\mathrm{16}}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{4}} \\ $$$$\:\frac{\mathrm{12}{r}}{\:\sqrt{\mathrm{6}}}\:+\:\mathrm{2}\sqrt{\frac{\mathrm{3}{r}\sqrt{\mathrm{6}}}{\mathrm{4}}}\:=\:\mathrm{9} \\ $$$$\:\mathrm{2}{r}\sqrt{\mathrm{6}}\:+\:\sqrt{\mathrm{3}{r}\sqrt{\mathrm{6}}}\:=\:\mathrm{9} \\ $$$$\:\mathrm{3}{r}\sqrt{\mathrm{6}}\:=\:\left(\mathrm{9}−\mathrm{2}{r}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} \\ $$$$\:\mathrm{3}{r}\sqrt{\mathrm{6}}\:=\:\mathrm{81}\:+\:\mathrm{24}{r}^{\mathrm{2}} \:−\:\mathrm{36}{r}\sqrt{\mathrm{6}} \\ $$$$\:\mathrm{24}{r}^{\mathrm{2}} −\mathrm{39}{r}\sqrt{\mathrm{6}}\:+\:\mathrm{81}\:=\:\mathrm{0} \\ $$$$\:\mathrm{8}{r}^{\mathrm{2}} −\mathrm{13}{r}\sqrt{\mathrm{6}}\:+\:\mathrm{27}\:=\:\mathrm{0}\: \\ $$$$\:{r}\:=\:\frac{\mathrm{13}\sqrt{\mathrm{6}}\pm\sqrt{\mathrm{169}\centerdot\mathrm{6}−\mathrm{4}\left(\mathrm{8}\right)\left(\mathrm{27}\right)}}{\mathrm{16}}\:=\:\frac{\mathrm{13}\sqrt{\mathrm{6}}\pm\sqrt{\mathrm{6}\centerdot\mathrm{169}−\mathrm{6}\centerdot\mathrm{144}}}{\mathrm{16}} \\ $$$$\:=\:\frac{\mathrm{13}\sqrt{\mathrm{6}}\pm\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{16}}\:\: \\ $$$$\:{R}\:>\:{r}\:\Rightarrow\:{r}\:\:=\:\frac{\sqrt{\mathrm{6}}}{\mathrm{2}};\: \\ $$
Commented by Rupesh123 last updated on 23/Feb/23
Very nice solution!
Commented by HeferH last updated on 23/Feb/23

Commented by Rupesh123 last updated on 23/Feb/23
Very detailed, sir
