Menu Close

Question-18798

Tinku Tara 0 Comments
Pin




Question Number 18798 by chernoaguero@gmail.com last updated on 29/Jul/17
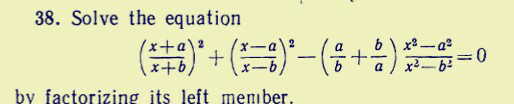
Answered by behi.8.3.4.1.7@gmail.com last updated on 30/Jul/17
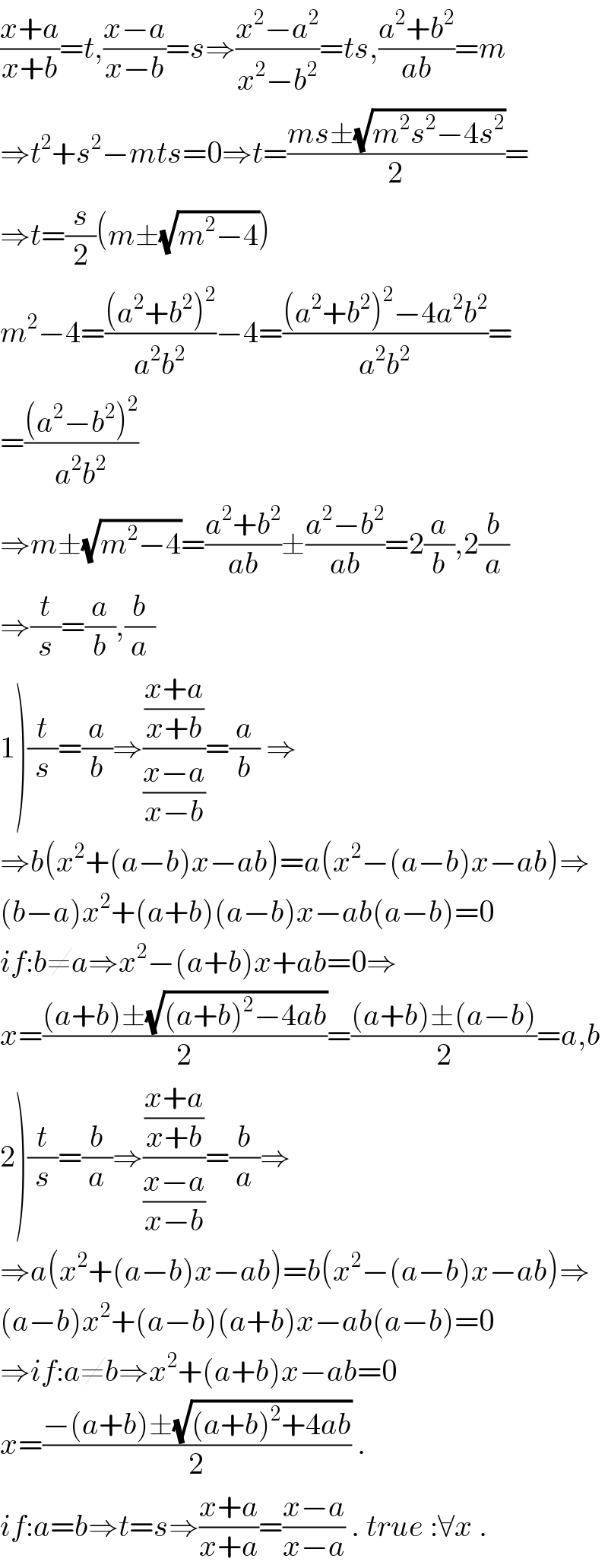
((x+a)/(x+b))=t,((x−a)/(x−b))=s⇒((x^2 −a^2 )/(x^2 −b^2 ))=ts,((a^2 +b^2 )/(ab))=m ⇒t^2 +s^2 −mts=0⇒t=((ms±(√(m^2 s^2 −4s^2 )))/2)= ⇒t=(s/2)(m±(√(m^2 −4))) m^2 −4=(((a^2 +b^2 )^2 )/(a^2 b^2 ))−4=(((a^2 +b^2 )^2 −4a^2 b^2 )/(a^2 b^2 ))= =(((a^2 −b^2 )^2 )/(a^2 b^2 )) ⇒m±(√(m^2 −4))=((a^2 +b^2 )/(ab))±((a^2 −b^2 )/(ab))=2(a/b),2(b/a) ⇒(t/s)=(a/b),(b/a) 1)(t/s)=(a/b)⇒(((x+a)/(x+b))/((x−a)/(x−b)))=(a/b) ⇒ ⇒b(x^2 +(a−b)x−ab)=a(x^2 −(a−b)x−ab)⇒ (b−a)x^2 +(a+b)(a−b)x−ab(a−b)=0 if:b≠a⇒x^2 −(a+b)x+ab=0⇒ x=(((a+b)±(√((a+b)^2 −4ab)))/2)=(((a+b)±(a−b))/2)=a,b 2)(t/s)=(b/a)⇒(((x+a)/(x+b))/((x−a)/(x−b)))=(b/a)⇒ ⇒a(x^2 +(a−b)x−ab)=b(x^2 −(a−b)x−ab)⇒ (a−b)x^2 +(a−b)(a+b)x−ab(a−b)=0 ⇒if:a≠b⇒x^2 +(a+b)x−ab=0 x=((−(a+b)±(√((a+b)^2 +4ab)))/2) . if:a=b⇒t=s⇒((x+a)/(x+a))=((x−a)/(x−a)) . true :∀x .
$$\frac{{x}+{a}}{{x}+{b}}={t},\frac{{x}−{a}}{{x}−{b}}={s}\Rightarrow\frac{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} −{b}^{\mathrm{2}} }={ts},\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{ab}}={m} \\ $$$$\Rightarrow{t}^{\mathrm{2}} +{s}^{\mathrm{2}} −{mts}=\mathrm{0}\Rightarrow{t}=\frac{{ms}\pm\sqrt{{m}^{\mathrm{2}} {s}^{\mathrm{2}} −\mathrm{4}{s}^{\mathrm{2}} }}{\mathrm{2}}= \\ $$$$\Rightarrow{t}=\frac{{s}}{\mathrm{2}}\left({m}\pm\sqrt{{m}^{\mathrm{2}} −\mathrm{4}}\right) \\ $$$${m}^{\mathrm{2}} −\mathrm{4}=\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }−\mathrm{4}=\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }= \\ $$$$=\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$$$\Rightarrow{m}\pm\sqrt{{m}^{\mathrm{2}} −\mathrm{4}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{ab}}\pm\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{ab}}=\mathrm{2}\frac{{a}}{{b}},\mathrm{2}\frac{{b}}{{a}} \\ $$$$\Rightarrow\frac{{t}}{{s}}=\frac{{a}}{{b}},\frac{{b}}{{a}} \\ $$$$\left.\mathrm{1}\right)\frac{{t}}{{s}}=\frac{{a}}{{b}}\Rightarrow\frac{\frac{{x}+{a}}{{x}+{b}}}{\frac{{x}−{a}}{{x}−{b}}}=\frac{{a}}{{b}}\:\Rightarrow \\ $$$$\Rightarrow{b}\left({x}^{\mathrm{2}} +\left({a}−{b}\right){x}−{ab}\right)={a}\left({x}^{\mathrm{2}} −\left({a}−{b}\right){x}−{ab}\right)\Rightarrow \\ $$$$\left({b}−{a}\right){x}^{\mathrm{2}} +\left({a}+{b}\right)\left({a}−{b}\right){x}−{ab}\left({a}−{b}\right)=\mathrm{0} \\ $$$${if}:{b}\neq{a}\Rightarrow{x}^{\mathrm{2}} −\left({a}+{b}\right){x}+{ab}=\mathrm{0}\Rightarrow \\ $$$${x}=\frac{\left({a}+{b}\right)\pm\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{4}{ab}}}{\mathrm{2}}=\frac{\left({a}+{b}\right)\pm\left({a}−{b}\right)}{\mathrm{2}}={a},{b} \\ $$$$\left.\mathrm{2}\right)\frac{{t}}{{s}}=\frac{{b}}{{a}}\Rightarrow\frac{\frac{{x}+{a}}{{x}+{b}}}{\frac{{x}−{a}}{{x}−{b}}}=\frac{{b}}{{a}}\Rightarrow \\ $$$$\Rightarrow{a}\left({x}^{\mathrm{2}} +\left({a}−{b}\right){x}−{ab}\right)={b}\left({x}^{\mathrm{2}} −\left({a}−{b}\right){x}−{ab}\right)\Rightarrow \\ $$$$\left({a}−{b}\right){x}^{\mathrm{2}} +\left({a}−{b}\right)\left({a}+{b}\right){x}−{ab}\left({a}−{b}\right)=\mathrm{0} \\ $$$$\Rightarrow{if}:{a}\neq{b}\Rightarrow{x}^{\mathrm{2}} +\left({a}+{b}\right){x}−{ab}=\mathrm{0} \\ $$$${x}=\frac{−\left({a}+{b}\right)\pm\sqrt{\left({a}+{b}\right)^{\mathrm{2}} +\mathrm{4}{ab}}}{\mathrm{2}}\:. \\ $$$${if}:{a}={b}\Rightarrow{t}={s}\Rightarrow\frac{{x}+{a}}{{x}+{a}}=\frac{{x}−{a}}{{x}−{a}}\:.\:{true}\::\forall{x}\:. \\ $$
Commented by chernoaguero@gmail.com last updated on 30/Jul/17
thanks sir i really appreciate it
$${thanks}\:{sir}\:{i}\:{really}\:{appreciate}\:{it} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *