Question Number 18818 by khamizan833@yahoo.com last updated on 30/Jul/17
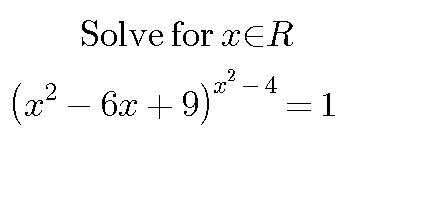
Answered by daffa22 last updated on 30/Jul/17
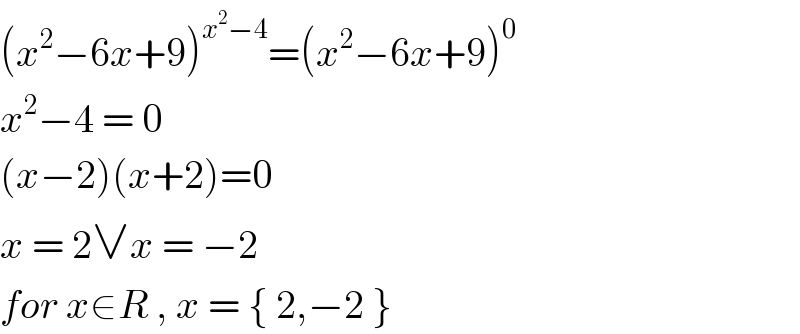
$$\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}\right)^{{x}^{\mathrm{2}} −\mathrm{4}} =\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9}\right)^{\mathrm{0}} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}\:=\:\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right)=\mathrm{0} \\ $$$${x}\:=\:\mathrm{2}\vee{x}\:=\:−\mathrm{2} \\ $$$${for}\:{x}\in{R}\:,\:{x}\:=\:\left\{\:\mathrm{2},−\mathrm{2}\:\right\} \\ $$
Commented by khamizan833@yahoo.com last updated on 30/Jul/17

$$\mathrm{Good}\:\mathrm{job}\:\mathrm{brothee}. \\ $$$$\mathrm{thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{solution}. \\ $$
Commented by daffa22 last updated on 30/Jul/17

$${sorry}\:{i}\:{made}\:{a}\:{mistake}, \\ $$$${i}\:{don}'{t}\:{know}\:{what}\:{x}\in{R}\:{means}, \\ $$$${thanks}\:{for}\:{your}\:{comment} \\ $$
Commented by FilupS last updated on 30/Jul/17
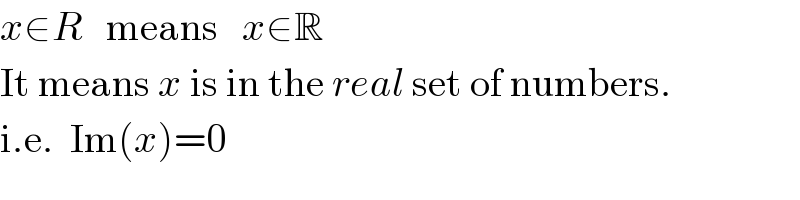
$${x}\in{R}\:\:\:\mathrm{means}\:\:\:{x}\in\mathbb{R} \\ $$$$\mathrm{It}\:\mathrm{means}\:{x}\:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:{real}\:\mathrm{set}\:\mathrm{of}\:\mathrm{numbers}. \\ $$$$\mathrm{i}.\mathrm{e}.\:\:\mathrm{Im}\left({x}\right)=\mathrm{0} \\ $$
Answered by mrW1 last updated on 30/Jul/17

$$\left(\mathrm{1}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}=\pm\mathrm{2} \\ $$$$\left(\mathrm{2}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{9}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}−\mathrm{3}=\pm\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{3}\pm\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{4},\mathrm{2} \\ $$$$\left(\mathrm{3}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{9}=−\mathrm{1}\:\mathrm{and}\:\mathrm{x}^{\mathrm{2}} −\mathrm{4}=\mathrm{even} \\ $$$$\Rightarrow\mathrm{no}\:\mathrm{real}\:\mathrm{solution} \\ $$$$ \\ $$$$\mathrm{all}\:\mathrm{solutions}: \\ $$$$\mathrm{x}=−\mathrm{2},\mathrm{2},\mathrm{4} \\ $$
Commented by khamizan833@yahoo.com last updated on 30/Jul/17

$$\mathrm{agree}\:\mathrm{with}\:\mathrm{your}\:\mathrm{solution}. \\ $$$$\mathrm{thank}\:\mathrm{mr}. \\ $$
