Question Number 188219 by Rupesh123 last updated on 26/Feb/23
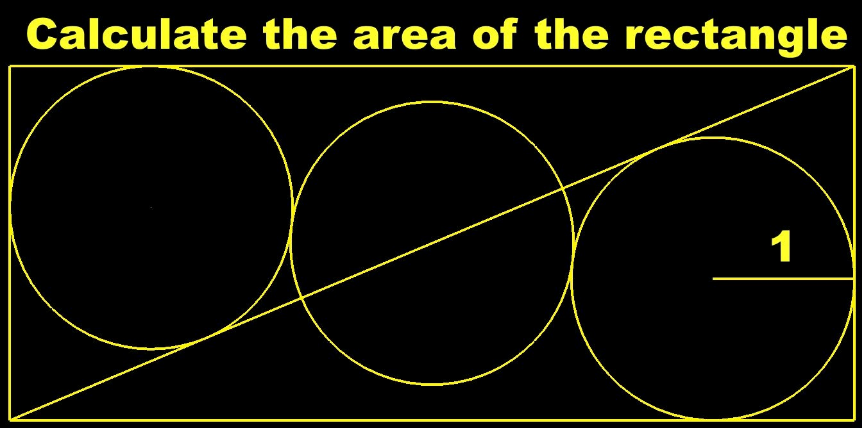
Answered by mr W last updated on 26/Feb/23

Commented by mr W last updated on 27/Feb/23

$$\mathrm{2}\beta+\alpha=\frac{\pi}{\mathrm{2}}\:\Rightarrow\beta=\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}} \\ $$$${length}\:{of}\:{rectangle}={a} \\ $$$${height}\:{of}\:{rectangle}={b} \\ $$$${a}=\mathrm{2}+\mathrm{4}\:\mathrm{cos}\:\left(\mathrm{30}°−\alpha\right) \\ $$$${b}=\mathrm{2}+\mathrm{4}\:\mathrm{sin}\:\left(\mathrm{30}°−\alpha\right) \\ $$$$\mathrm{2}\left(\sqrt{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{tan}\:\beta}\right)\mathrm{sin}\:\alpha=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\beta} \\ $$$$\mathrm{2}\left(\sqrt{\mathrm{3}}+\frac{\mathrm{1}+\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}\right)×\frac{\mathrm{2}\:\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}}=\mathrm{1}+\frac{\mathrm{1}+\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}} \\ $$$$\mathrm{2}\left(\sqrt{\mathrm{3}}+\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\right)×\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }=\mathrm{1}+\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}} \\ $$$$\left(\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}\right){t}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{1}=\mathrm{0} \\ $$$${t}=\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\frac{\mathrm{1}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{7}}}{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}} \\ $$$$\Rightarrow\alpha=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{7}}}{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}\right)\approx\mathrm{21}.\mathrm{067630} \\ $$$${a}\approx\mathrm{5}.\mathrm{951489} \\ $$$${b}\approx\mathrm{2}.\mathrm{621074} \\ $$$${A}\approx\mathrm{15}.\mathrm{599293} \\ $$
Commented by Rupesh123 last updated on 26/Feb/23
Very detailed solution!
Perfect Explanation!
