Question Number 188378 by Mingma last updated on 28/Feb/23
Answered by HeferH last updated on 09/Mar/23

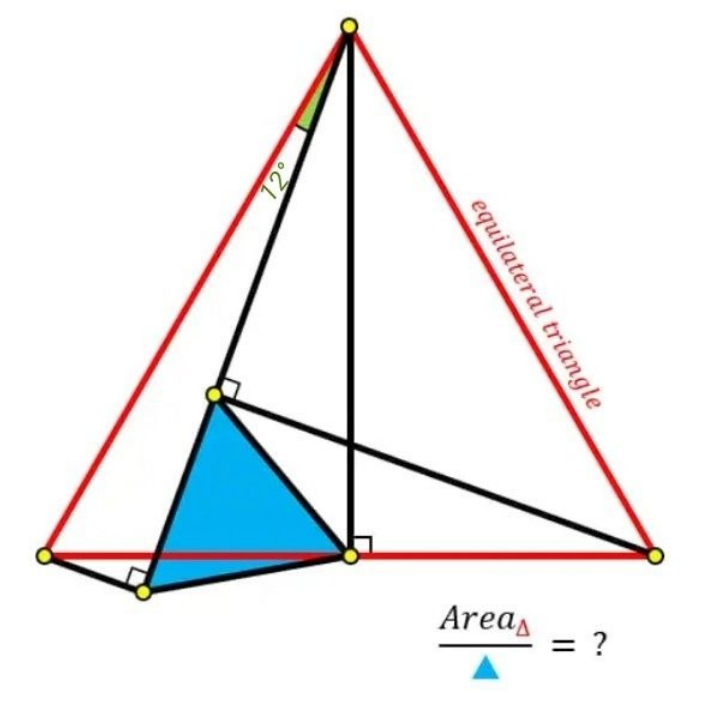
$${let}\:{x}\:{be}\:{the}\:{side}\:{of}\:{the}\:{red}\:{triangle}\:{and}\:{y}\:{be}\:{the} \\ $$$${side}\:{of}\:{the}\:{blue}\:{one} \\ $$$$\:\mathrm{sin}\:\left(\mathrm{18}°\right)\:=\:\frac{{y}}{{x}}\: \\ $$$$\frac{{A}_{{r}} }{{A}_{{b}} }\:=\:\left(\frac{\mathrm{1}}{\mathrm{sin}\:\left(\mathrm{18}°\right)}\right)^{\mathrm{2}} \:=\:\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} \:=\:\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}\right)^{\mathrm{2}} =\:\frac{\mathrm{8}}{\mathrm{3}−\sqrt{\mathrm{5}}} \\ $$$$\:=\:\frac{\mathrm{8}\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)}{\mathrm{9}−\mathrm{5}}\:=\:\mathrm{2}\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)=\:\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}} \\ $$
