Menu Close

Question-188508

Tinku Tara 0 Comments
Pin




Question Number 188508 by Rupesh123 last updated on 02/Mar/23
Answered by som(math1967) last updated on 02/Mar/23
a^3 +b^3 +c^3 −3abc=0 ⇒(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)=0 ⇒a^2 +b^2 +c^2 −ab−bc−ca=0 [(a+b+c)≠0] ⇒2a^2 +2b^2 +2c^2 −2ab−2bc−2ca=0 ⇒(a−b)^2 +(b−c)^2 +(c−a)^2 =0 for real value of a,b,c (a−b)^2 =0⇒a−b=0⇒a=b (b−c)^2 ⇒b=c ∴a=b=c ((a^2 +b^2 +c^2 )/((a+b+c)^2 ))=((3a^2 )/(9a^2 ))=(1/3)
$$\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}=\mathrm{0} \\ $$$$\Rightarrow\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}\right)=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}=\mathrm{0} \\ $$$$\left[\left({a}+{b}+{c}\right)\neq\mathrm{0}\right] \\ $$$$\Rightarrow\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{2}} −\mathrm{2}{ab}−\mathrm{2}{bc}−\mathrm{2}{ca}=\mathrm{0} \\ $$$$\Rightarrow\left({a}−{b}\right)^{\mathrm{2}} +\left({b}−{c}\right)^{\mathrm{2}} +\left({c}−{a}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${for}\:{real}\:{value}\:{of}\:{a},{b},{c} \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow{a}−{b}=\mathrm{0}\Rightarrow{a}={b} \\ $$$$\left({b}−{c}\right)^{\mathrm{2}} \Rightarrow{b}={c} \\ $$$$\therefore{a}={b}={c} \\ $$$$\:\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\left({a}+{b}+{c}\right)^{\mathrm{2}} }=\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{9}{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Rupesh123 last updated on 02/Mar/23
Excellent
Answered by Rasheed.Sindhi last updated on 02/Mar/23
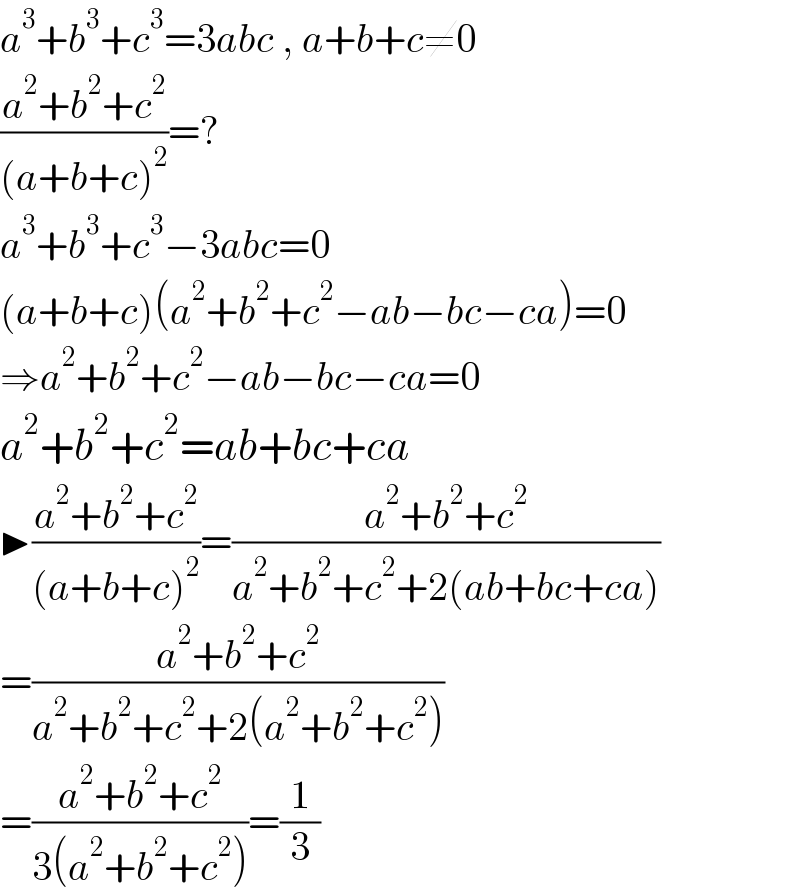
a^3 +b^3 +c^3 =3abc , a+b+c≠0 ((a^2 +b^2 +c^2 )/((a+b+c)^2 ))=? a^3 +b^3 +c^3 −3abc=0 (a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)=0 ⇒a^2 +b^2 +c^2 −ab−bc−ca=0 a^2 +b^2 +c^2 =ab+bc+ca ▶((a^2 +b^2 +c^2 )/((a+b+c)^2 ))=((a^2 +b^2 +c^2 )/(a^2 +b^2 +c^2 +2(ab+bc+ca))) =((a^2 +b^2 +c^2 )/(a^2 +b^2 +c^2 +2(a^2 +b^2 +c^2 ))) =((a^2 +b^2 +c^2 )/(3(a^2 +b^2 +c^2 )))=(1/3)
$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{3}{abc}\:,\:{a}+{b}+{c}\neq\mathrm{0} \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\left({a}+{b}+{c}\right)^{\mathrm{2}} }=? \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}=\mathrm{0} \\ $$$$\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}\right)=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} ={ab}+{bc}+{ca} \\ $$$$\blacktriangleright\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\left({a}+{b}+{c}\right)^{\mathrm{2}} }=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right)} \\ $$$$=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)} \\ $$$$=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Rupesh123 last updated on 02/Mar/23
Excellent

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *