Menu Close

Question-18864

Tinku Tara 0 Comments
Pin




Question Number 18864 by chernoaguero@gmail.com last updated on 31/Jul/17
Commented by mrW1 last updated on 31/Jul/17
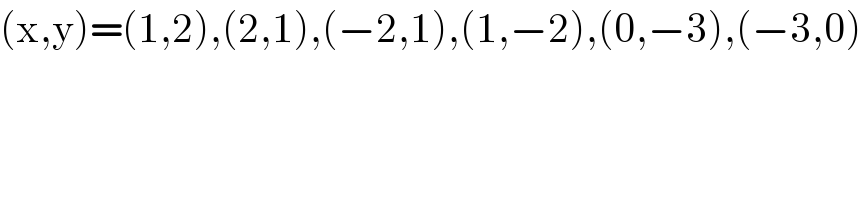
(x,y)=(1,2),(2,1),(−2,1),(1,−2),(0,−3),(−3,0)
$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{2},\mathrm{1}\right),\left(−\mathrm{2},\mathrm{1}\right),\left(\mathrm{1},−\mathrm{2}\right),\left(\mathrm{0},−\mathrm{3}\right),\left(−\mathrm{3},\mathrm{0}\right) \\ $$
Answered by behi.8.3.4.1.7@gmail.com last updated on 31/Jul/17
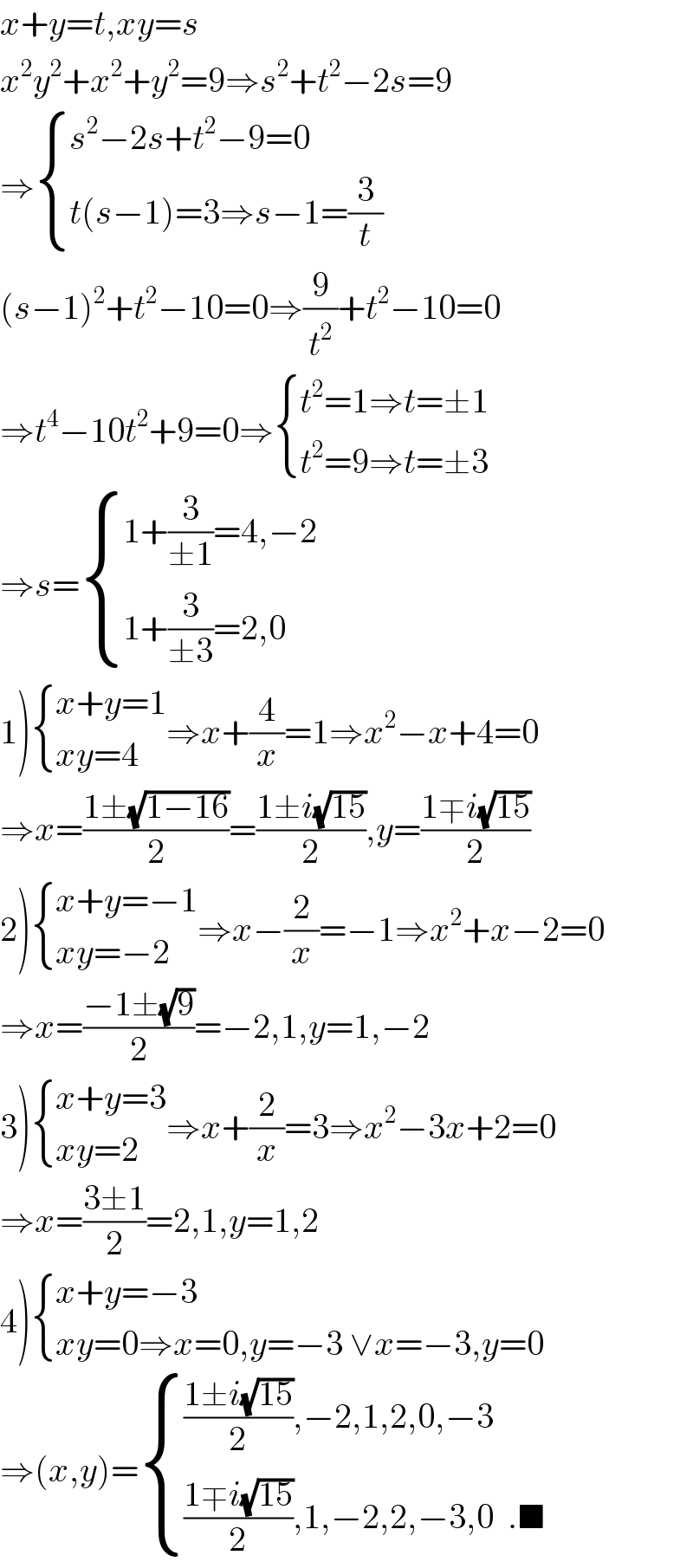
x+y=t,xy=s x^2 y^2 +x^2 +y^2 =9⇒s^2 +t^2 −2s=9 ⇒ { ((s^2 −2s+t^2 −9=0)),((t(s−1)=3⇒s−1=(3/t))) :} (s−1)^2 +t^2 −10=0⇒(9/t^2 )+t^2 −10=0 ⇒t^4 −10t^2 +9=0⇒ { ((t^2 =1⇒t=±1)),((t^2 =9⇒t=±3)) :} ⇒s= { ((1+(3/(±1))=4,−2)),((1+(3/(±3))=2,0)) :} 1) { ((x+y=1)),((xy=4)) :}⇒x+(4/x)=1⇒x^2 −x+4=0 ⇒x=((1±(√(1−16)))/2)=((1±i(√(15)))/2),y=((1∓i(√(15)))/2) 2) { ((x+y=−1)),((xy=−2)) :}⇒x−(2/x)=−1⇒x^2 +x−2=0 ⇒x=((−1±(√9))/2)=−2,1,y=1,−2 3) { ((x+y=3)),((xy=2)) :}⇒x+(2/x)=3⇒x^2 −3x+2=0 ⇒x=((3±1)/2)=2,1,y=1,2 4) { ((x+y=−3)),((xy=0⇒x=0,y=−3 ∨x=−3,y=0)) :} ⇒(x,y)= { ((((1±i(√(15)))/2),−2,1,2,0,−3)),((((1∓i(√(15)))/2),1,−2,2,−3,0 .■)) :}
$${x}+{y}={t},{xy}={s} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{9}\Rightarrow{s}^{\mathrm{2}} +{t}^{\mathrm{2}} −\mathrm{2}{s}=\mathrm{9} \\ $$$$\Rightarrow\begin{cases}{{s}^{\mathrm{2}} −\mathrm{2}{s}+{t}^{\mathrm{2}} −\mathrm{9}=\mathrm{0}}\\{{t}\left({s}−\mathrm{1}\right)=\mathrm{3}\Rightarrow{s}−\mathrm{1}=\frac{\mathrm{3}}{{t}}}\end{cases} \\ $$$$\left({s}−\mathrm{1}\right)^{\mathrm{2}} +{t}^{\mathrm{2}} −\mathrm{10}=\mathrm{0}\Rightarrow\frac{\mathrm{9}}{{t}^{\mathrm{2}} }+{t}^{\mathrm{2}} −\mathrm{10}=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{4}} −\mathrm{10}{t}^{\mathrm{2}} +\mathrm{9}=\mathrm{0}\Rightarrow\begin{cases}{{t}^{\mathrm{2}} =\mathrm{1}\Rightarrow{t}=\pm\mathrm{1}}\\{{t}^{\mathrm{2}} =\mathrm{9}\Rightarrow{t}=\pm\mathrm{3}}\end{cases} \\ $$$$\Rightarrow{s}=\begin{cases}{\mathrm{1}+\frac{\mathrm{3}}{\pm\mathrm{1}}=\mathrm{4},−\mathrm{2}}\\{\mathrm{1}+\frac{\mathrm{3}}{\pm\mathrm{3}}=\mathrm{2},\mathrm{0}}\end{cases} \\ $$$$\left.\mathrm{1}\right)\begin{cases}{{x}+{y}=\mathrm{1}}\\{{xy}=\mathrm{4}}\end{cases}\Rightarrow{x}+\frac{\mathrm{4}}{{x}}=\mathrm{1}\Rightarrow{x}^{\mathrm{2}} −{x}+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{16}}}{\mathrm{2}}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{15}}}{\mathrm{2}},{y}=\frac{\mathrm{1}\mp{i}\sqrt{\mathrm{15}}}{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\begin{cases}{{x}+{y}=−\mathrm{1}}\\{{xy}=−\mathrm{2}}\end{cases}\Rightarrow{x}−\frac{\mathrm{2}}{{x}}=−\mathrm{1}\Rightarrow{x}^{\mathrm{2}} +{x}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{9}}}{\mathrm{2}}=−\mathrm{2},\mathrm{1},{y}=\mathrm{1},−\mathrm{2} \\ $$$$\left.\mathrm{3}\right)\begin{cases}{{x}+{y}=\mathrm{3}}\\{{xy}=\mathrm{2}}\end{cases}\Rightarrow{x}+\frac{\mathrm{2}}{{x}}=\mathrm{3}\Rightarrow{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}\pm\mathrm{1}}{\mathrm{2}}=\mathrm{2},\mathrm{1},{y}=\mathrm{1},\mathrm{2} \\ $$$$\left.\mathrm{4}\right)\begin{cases}{{x}+{y}=−\mathrm{3}}\\{{xy}=\mathrm{0}\Rightarrow{x}=\mathrm{0},{y}=−\mathrm{3}\:\vee{x}=−\mathrm{3},{y}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\left({x},{y}\right)=\begin{cases}{\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{15}}}{\mathrm{2}},−\mathrm{2},\mathrm{1},\mathrm{2},\mathrm{0},−\mathrm{3}}\\{\frac{\mathrm{1}\mp{i}\sqrt{\mathrm{15}}}{\mathrm{2}},\mathrm{1},−\mathrm{2},\mathrm{2},−\mathrm{3},\mathrm{0}\:\:.\blacksquare}\end{cases} \\ $$
Commented by chernoaguero@gmail.com last updated on 31/Jul/17
thankz sir
$${thankz}\:{sir} \\ $$
Answered by mrW1 last updated on 31/Jul/17
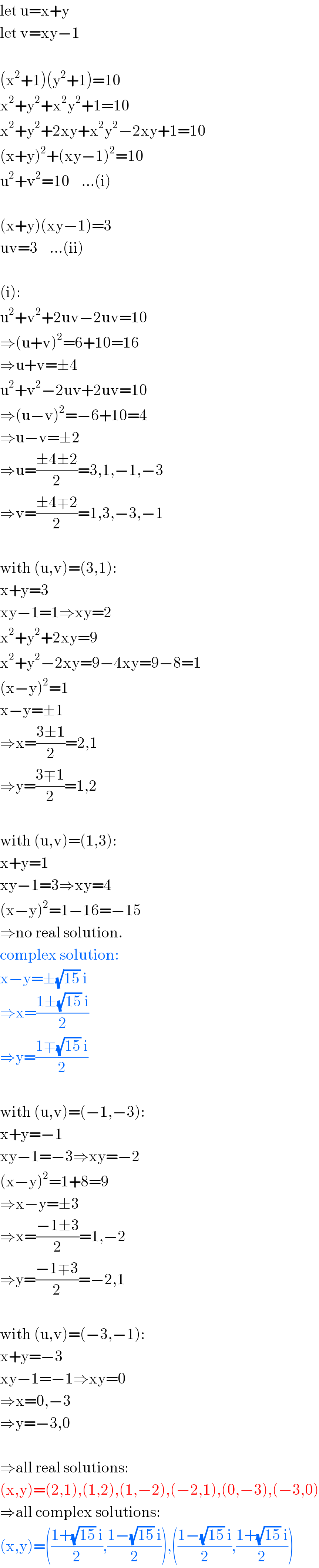
let u=x+y let v=xy−1 (x^2 +1)(y^2 +1)=10 x^2 +y^2 +x^2 y^2 +1=10 x^2 +y^2 +2xy+x^2 y^2 −2xy+1=10 (x+y)^2 +(xy−1)^2 =10 u^2 +v^2 =10 ...(i) (x+y)(xy−1)=3 uv=3 ...(ii) (i): u^2 +v^2 +2uv−2uv=10 ⇒(u+v)^2 =6+10=16 ⇒u+v=±4 u^2 +v^2 −2uv+2uv=10 ⇒(u−v)^2 =−6+10=4 ⇒u−v=±2 ⇒u=((±4±2)/2)=3,1,−1,−3 ⇒v=((±4∓2)/2)=1,3,−3,−1 with (u,v)=(3,1): x+y=3 xy−1=1⇒xy=2 x^2 +y^2 +2xy=9 x^2 +y^2 −2xy=9−4xy=9−8=1 (x−y)^2 =1 x−y=±1 ⇒x=((3±1)/2)=2,1 ⇒y=((3∓1)/2)=1,2 with (u,v)=(1,3): x+y=1 xy−1=3⇒xy=4 (x−y)^2 =1−16=−15 ⇒no real solution. complex solution: x−y=±(√(15)) i ⇒x=((1±(√(15)) i)/2) ⇒y=((1∓(√(15)) i)/2) with (u,v)=(−1,−3): x+y=−1 xy−1=−3⇒xy=−2 (x−y)^2 =1+8=9 ⇒x−y=±3 ⇒x=((−1±3)/2)=1,−2 ⇒y=((−1∓3)/2)=−2,1 with (u,v)=(−3,−1): x+y=−3 xy−1=−1⇒xy=0 ⇒x=0,−3 ⇒y=−3,0 ⇒all real solutions: (x,y)=(2,1),(1,2),(1,−2),(−2,1),(0,−3),(−3,0) ⇒all complex solutions: (x,y)=(((1+(√(15)) i)/2),((1−(√(15)) i)/2)),(((1−(√(15)) i)/2),((1+(√(15)) i)/2))
$$\mathrm{let}\:\mathrm{u}=\mathrm{x}+\mathrm{y} \\ $$$$\mathrm{let}\:\mathrm{v}=\mathrm{xy}−\mathrm{1} \\ $$$$ \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{10} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{1}=\mathrm{10} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} −\mathrm{2xy}+\mathrm{1}=\mathrm{10} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} +\left(\mathrm{xy}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{10} \\ $$$$\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} =\mathrm{10}\:\:\:\:…\left(\mathrm{i}\right) \\ $$$$ \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{xy}−\mathrm{1}\right)=\mathrm{3} \\ $$$$\mathrm{uv}=\mathrm{3}\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$$ \\ $$$$\left(\mathrm{i}\right): \\ $$$$\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} +\mathrm{2uv}−\mathrm{2uv}=\mathrm{10} \\ $$$$\Rightarrow\left(\mathrm{u}+\mathrm{v}\right)^{\mathrm{2}} =\mathrm{6}+\mathrm{10}=\mathrm{16} \\ $$$$\Rightarrow\mathrm{u}+\mathrm{v}=\pm\mathrm{4} \\ $$$$\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} −\mathrm{2uv}+\mathrm{2uv}=\mathrm{10} \\ $$$$\Rightarrow\left(\mathrm{u}−\mathrm{v}\right)^{\mathrm{2}} =−\mathrm{6}+\mathrm{10}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{u}−\mathrm{v}=\pm\mathrm{2} \\ $$$$\Rightarrow\mathrm{u}=\frac{\pm\mathrm{4}\pm\mathrm{2}}{\mathrm{2}}=\mathrm{3},\mathrm{1},−\mathrm{1},−\mathrm{3} \\ $$$$\Rightarrow\mathrm{v}=\frac{\pm\mathrm{4}\mp\mathrm{2}}{\mathrm{2}}=\mathrm{1},\mathrm{3},−\mathrm{3},−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{with}\:\left(\mathrm{u},\mathrm{v}\right)=\left(\mathrm{3},\mathrm{1}\right): \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{3} \\ $$$$\mathrm{xy}−\mathrm{1}=\mathrm{1}\Rightarrow\mathrm{xy}=\mathrm{2} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{2xy}=\mathrm{9} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2xy}=\mathrm{9}−\mathrm{4xy}=\mathrm{9}−\mathrm{8}=\mathrm{1} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{x}−\mathrm{y}=\pm\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{3}\pm\mathrm{1}}{\mathrm{2}}=\mathrm{2},\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{3}\mp\mathrm{1}}{\mathrm{2}}=\mathrm{1},\mathrm{2} \\ $$$$ \\ $$$$\mathrm{with}\:\left(\mathrm{u},\mathrm{v}\right)=\left(\mathrm{1},\mathrm{3}\right): \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{1} \\ $$$$\mathrm{xy}−\mathrm{1}=\mathrm{3}\Rightarrow\mathrm{xy}=\mathrm{4} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{16}=−\mathrm{15} \\ $$$$\Rightarrow\mathrm{no}\:\mathrm{real}\:\mathrm{solution}. \\ $$$$\mathrm{complex}\:\mathrm{solution}: \\ $$$$\mathrm{x}−\mathrm{y}=\pm\sqrt{\mathrm{15}}\:\mathrm{i} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{15}}\:\mathrm{i}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{1}\mp\sqrt{\mathrm{15}}\:\mathrm{i}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{with}\:\left(\mathrm{u},\mathrm{v}\right)=\left(−\mathrm{1},−\mathrm{3}\right): \\ $$$$\mathrm{x}+\mathrm{y}=−\mathrm{1} \\ $$$$\mathrm{xy}−\mathrm{1}=−\mathrm{3}\Rightarrow\mathrm{xy}=−\mathrm{2} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{8}=\mathrm{9} \\ $$$$\Rightarrow\mathrm{x}−\mathrm{y}=\pm\mathrm{3} \\ $$$$\Rightarrow\mathrm{x}=\frac{−\mathrm{1}\pm\mathrm{3}}{\mathrm{2}}=\mathrm{1},−\mathrm{2} \\ $$$$\Rightarrow\mathrm{y}=\frac{−\mathrm{1}\mp\mathrm{3}}{\mathrm{2}}=−\mathrm{2},\mathrm{1} \\ $$$$ \\ $$$$\mathrm{with}\:\left(\mathrm{u},\mathrm{v}\right)=\left(−\mathrm{3},−\mathrm{1}\right): \\ $$$$\mathrm{x}+\mathrm{y}=−\mathrm{3} \\ $$$$\mathrm{xy}−\mathrm{1}=−\mathrm{1}\Rightarrow\mathrm{xy}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{0},−\mathrm{3} \\ $$$$\Rightarrow\mathrm{y}=−\mathrm{3},\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow\mathrm{all}\:\mathrm{real}\:\mathrm{solutions}: \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{2},\mathrm{1}\right),\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{1},−\mathrm{2}\right),\left(−\mathrm{2},\mathrm{1}\right),\left(\mathrm{0},−\mathrm{3}\right),\left(−\mathrm{3},\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{all}\:\mathrm{complex}\:\mathrm{solutions}: \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\frac{\mathrm{1}+\sqrt{\mathrm{15}}\:\mathrm{i}}{\mathrm{2}},\frac{\mathrm{1}−\sqrt{\mathrm{15}}\:\mathrm{i}}{\mathrm{2}}\right),\left(\frac{\mathrm{1}−\sqrt{\mathrm{15}}\:\mathrm{i}}{\mathrm{2}},\frac{\mathrm{1}+\sqrt{\mathrm{15}}\:\mathrm{i}}{\mathrm{2}}\right) \\ $$
Commented by chernoaguero@gmail.com last updated on 31/Jul/17
Thankz sir
$${Thankz}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *