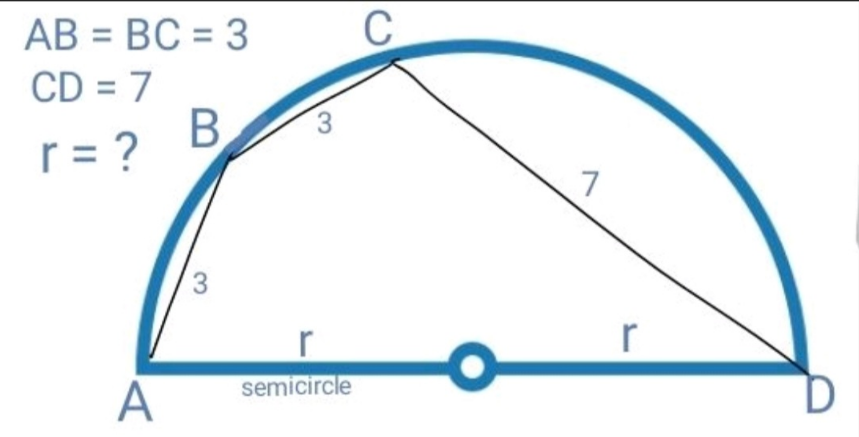
Question Number 188669 by Rupesh123 last updated on 04/Mar/23
Answered by HeferH last updated on 04/Mar/23

$$\mathrm{9}−\left({r}−\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} =\:{r}^{\mathrm{2}} −\left(\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${r}\:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$
Answered by cortano12 last updated on 05/Mar/23

$$\:\Rightarrow\mathrm{7}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\frac{\mathrm{7}.\mathrm{3}.\mathrm{3}}{{r}}\:=\:\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{67}+\frac{\mathrm{63}}{\mathrm{r}}\:=\:\mathrm{4r}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4r}^{\mathrm{3}} −\mathrm{67r}−\mathrm{63}\:=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2r}−\mathrm{9}\right)\left(\mathrm{2r}+\mathrm{7}\right)\left(\mathrm{r}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{r}\:=\:\mathrm{4}.\mathrm{5}\: \\ $$
Answered by mr W last updated on 05/Mar/23

Commented by mr W last updated on 05/Mar/23

$${r}^{\mathrm{2}} −\left(\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} −\left({r}−\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{r}^{\mathrm{2}} −\mathrm{7}{r}−\mathrm{9}=\mathrm{0} \\ $$$${r}=\frac{\mathrm{7}+\mathrm{11}}{\mathrm{4}}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 05/Mar/23

Answered by cortano12 last updated on 05/Mar/23

$$\left(\bullet\right)\:\mathrm{BD}=\sqrt{\mathrm{d}^{\mathrm{2}} −\mathrm{9}} \\ $$$$\left(\bullet\right)\:\mathrm{AC}=\sqrt{\mathrm{d}^{\mathrm{2}} −\mathrm{49}} \\ $$$$\:\mathrm{By}\:\mathrm{Ptolomeus}\:\mathrm{Theorem}\: \\ $$$$\Rightarrow\mathrm{BC}.\mathrm{AD}+\mathrm{AB}.\mathrm{BC}\:=\:\mathrm{BD}.\mathrm{AC} \\ $$$$\Rightarrow\left(\mathrm{21}+\mathrm{3d}\right)^{\mathrm{2}} =\left(\mathrm{d}^{\mathrm{2}} −\mathrm{9}\right)\left(\mathrm{d}^{\mathrm{2}} −\mathrm{49}\right) \\ $$$$\Rightarrow\mathrm{d}\left(\mathrm{d}+\mathrm{7}\right)\left(\mathrm{d}+\mathrm{2}\right)\left(\mathrm{d}−\mathrm{9}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{d}=\mathrm{2r}\:=\:\mathrm{9}\:;\:\mathrm{r}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$
