Question Number 189049 by mr W last updated on 11/Mar/23
Commented by mr W last updated on 13/Mar/23

$${this}\:{is}\:{an}\:{old}\:{question}\:\left({Q}\mathrm{164560}\right).\: \\ $$$${maybe}\:{meanwhile}\:{somebody}\:{has}\:{got}\: \\ $$$${a}\:{new}\:{solution}. \\ $$
Commented by nikif99 last updated on 11/Mar/23

Answered by nikif99 last updated on 11/Mar/23
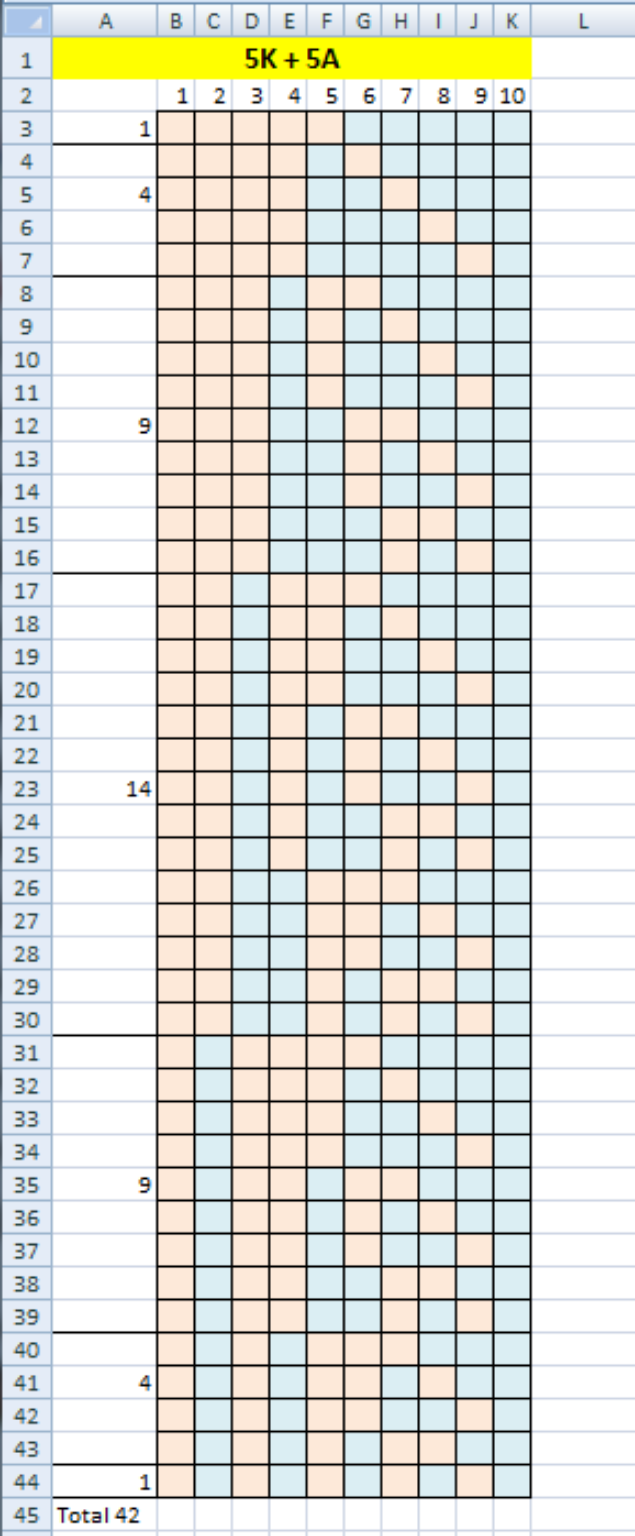
![132 At first, I tried to solve it graphically [see attached; every row is a queue of girls (pink) and boys (blue)] not creating problem to the cashier. Then, I tried to generalise the solution (5g+5b: 42; 4g+4b: 14) without succes. Later, I noticed a comment in a (greek) article about the principle of reflection in combinatorics with the solution: The probability for not problem to the cashier is 1/(n+1). Considering all possible arrangements in queue is C_n ^(2n) , the accepted queues are (1/(n+1)) C_n ^(2n) =(1/7)∙924=132](https://www.tinkutara.com/question/Q189084.png)
$$\mathrm{132} \\ $$$${At}\:{first},\:{I}\:{tried}\:{to}\:{solve}\:{it}\:{graphically}\: \\ $$$$\left[{see}\:{attached};\:{every}\:{row}\:{is}\:{a}\:{queue}\:\right. \\ $$$$\left.{of}\:{girls}\:\left({pink}\right)\:{and}\:{boys}\:\left({blue}\right)\right]\:{not} \\ $$$${creating}\:{problem}\:{to}\:{the}\:{cashier}. \\ $$$${Then},\:{I}\:{tried}\:{to}\:{generalise}\:{the}\:{solution} \\ $$$$\left(\mathrm{5}{g}+\mathrm{5}{b}:\:\mathrm{42};\:\mathrm{4}{g}+\mathrm{4}{b}:\:\mathrm{14}\right)\:{without}\:{succes}. \\ $$$${Later},\:{I}\:{noticed}\:{a}\:{comment}\:{in}\:{a}\:\left({greek}\right) \\ $$$${article}\:{about}\:{the}\:{principle}\:{of}\:{reflection} \\ $$$${in}\:{combinatorics}\:{with}\:{the}\:{solution}: \\ $$$${The}\:{probability}\:{for}\:{not}\:{problem}\:{to}\:{the} \\ $$$${cashier}\:{is}\:\mathrm{1}/\left({n}+\mathrm{1}\right). \\ $$$${Considering}\:{all}\:{possible}\:{arrangements} \\ $$$${in}\:{queue}\:{is}\:{C}_{{n}} ^{\mathrm{2}{n}} ,\:{the}\:{accepted}\:{queues}\:{are} \\ $$$$\frac{\mathrm{1}}{{n}+\mathrm{1}}\:{C}_{{n}} ^{\mathrm{2}{n}} \:=\frac{\mathrm{1}}{\mathrm{7}}\centerdot\mathrm{924}=\mathrm{132} \\ $$
Commented by nikif99 last updated on 11/Mar/23
Commented by nikif99 last updated on 11/Mar/23

Commented by manxsol last updated on 12/Mar/23

$${interesante}.{comand}\:{in}\: \\ $$$${excel}\:{creation}\:{table}\:.{please}\:{or} \\ $$$$\:\:{macro}.{thank}\:{Sr}\:{nikki}. \\ $$$${ah}\:{link}\:{article}? \\ $$
Commented by mr W last updated on 12/Mar/23

$$\underline{{my}\:{consideration}:} \\ $$$${at}\:{any}\:{point}\:{in}\:{the}\:{queue}\:{the}\:{total}\: \\ $$$${number}\:{of}\:{girls}\:{must}\:{be}\:{more}\:{than}\: \\ $$$${or}\:{equal}\:{to}\:{the}\:{total}\:{number}\:{of}\:{boys}.\: \\ $$$${we}\:{can}\:{display}\:{this}\:{as}\:{a}\:{step}\:{path}\:{like}\: \\ $$$${the}\:{following}\:{one}.\:\:{if}\:{such}\:{a}\:{path}\:{lies} \\ $$$${completely}\:{above}\:{the}\:{diagonal}\: \\ $$$$\left({shaded}\:{zone}\right),\:{then}\:{the}\:{cashier}\:{has}\: \\ $$$${no}\:{problem}\:{with}\:{change}. \\ $$
Commented by mr W last updated on 12/Mar/23

Commented by mr W last updated on 12/Mar/23

$${this}\:{example}\:{shows}\:{a}\:{path}\:{for}\:{the}\: \\ $$$${case}\:{with}\:\mathrm{6}\:{girls}\:{and}\:\mathrm{6}\:{boys}.\:{it}\: \\ $$$${represents}\:{the}\:{queue}:\:\mathrm{2}\:{girls},\:\mathrm{1}\:{boy},\: \\ $$$$\mathrm{1}\:{girl},\:\mathrm{2}\:{boys},\:\mathrm{2}\:{girls},\:\mathrm{1}\:{boy},\:\mathrm{1}\:{girl}\:{and} \\ $$$${finally}\:\mathrm{2}\:{boys}. \\ $$$${generally}\:{with}\:{n}\:{girls}\:{and}\:{n}\:{boys},\:{the} \\ $$$${number}\:{of}\:{valid}\:{paths}\:{is} \\ $$$${C}_{{n}} =\frac{{C}_{{n}} ^{\mathrm{2}{n}} }{{n}+\mathrm{1}}=\frac{\left(\mathrm{2}{n}\right)!}{\left({n}+\mathrm{1}\right)!{n}!} \\ $$$${which}\:{is}\:{the}\:{Catalan}\:{number}. \\ $$
Commented by mr W last updated on 12/Mar/23

Commented by mr W last updated on 12/Mar/23
https://mathshistory.st-andrews.ac.uk/Extras/Catalan/
Commented by mr W last updated on 12/Mar/23
https://en.m.wikipedia.org/wiki/Catalan_number
Commented by mr W last updated on 12/Mar/23

$${nikif}\:{sir}\:{has}\:{got}\:\mathrm{14}\:{for}\:{n}=\mathrm{4}\:{and}\:\mathrm{42} \\ $$$${for}\:{n}=\mathrm{5}\:{and}\:\mathrm{132}\:{for}\:{n}=\mathrm{6},\:{they}\:{are} \\ $$$${all}\:{correct}\:{and}\:{are}\:{the}\:{corresponding} \\ $$$${Catalan}\:{numbers}. \\ $$
Commented by nikif99 last updated on 12/Mar/23

$${Wonderful}\:{lesson}.\:{Thank}\:{you}\:{Sir}! \\ $$
Commented by manxsol last updated on 12/Mar/23

$${Thank}\:{you}\:{very}\:{much} \\ $$$$\:{Sir}.\:{W}\:{and}\:{Sr}.\:{Nikkif}\:{for} \\ $$$$\:{your}\:{effort}\:{and}\:\:{for}\:{sharing} \\ $$
Commented by nikif99 last updated on 12/Mar/23

$$@{manxsol} \\ $$$$−{no}\:{macro}\:{used}\:{in}\:{excel}.\:{Rows}\: \\ $$$${created}\:{manually}\:{in}\:{blocks},\:{following} \\ $$$${combination}\:{pattern}. \\ $$$$−{I}\:{have}\:{not}\:{the}\:{article},\:{just}\:{a}\:{picture} \\ $$$${kept}.\:{The}\:{problem}\:{is}\:{presented}\:{more} \\ $$$${complicated}.\:{Text}\:{says}: \\ $$$${There}\:{is}\:{a}\:{queue}\:{of}\:\mathrm{2}{n}\:{persons}\:{over}\:{the} \\ $$$${cashier}\:{of}\:{a}\:{theater}.\:{Half}\:{of}\:{them}\:{have} \\ $$$${only}\:{banknotes}\:{of}\:\mathrm{1000},\:{while}\:{the}\:{other} \\ $$$${half}\:{have}\:{some}\:\mathrm{1000}{s}\:{and}\:{only}\:{one} \\ $$$${banknote}\:{of}\:\mathrm{500}.\:{Tickets}\:{cost}\:\mathrm{2500}\:{and} \\ $$$$\mathrm{3500}.\:{The}\:{cashier}\:{has}\:{no}\:{money}\:{at} \\ $$$${the}\:{beginning}.\:{It}\:{is}\:{clear}\:{that}\:{they}\:{are} \\ $$$$\left(\begin{matrix}{\mathrm{2}{n}}\\{{n}}\end{matrix}\right)\:{ways}\:{to}\:{arrange}\:{in}\:{queue}. \\ $$$${In}\:{how}\:{many}\:{of}\:{these}\:{ways}\:{the}\:{cashier} \\ $$$${has}\:{always}\:\mathrm{500},\:{so}\:{no}\:{problem}\:{occurs}? \\ $$$${Frame}\:{bottom}\:{right}:\:{probability}\:{for} \\ $$$${no}\:{problem}:\:\mathrm{1}/\left({n}+\mathrm{1}\right). \\ $$
Commented by nikif99 last updated on 12/Mar/23

Commented by manxsol last updated on 12/Mar/23

$${thansSr}.{nikkifor}\:{dedicating} \\ $$$$\:{your}\:{time}\:{for}\:{my}\:{question} \\ $$
