Question Number 189539 by mokys last updated on 18/Mar/23

Commented by mokys last updated on 18/Mar/23

$${find}\:{x}\:? \\ $$
Commented by cortano12 last updated on 18/Mar/23
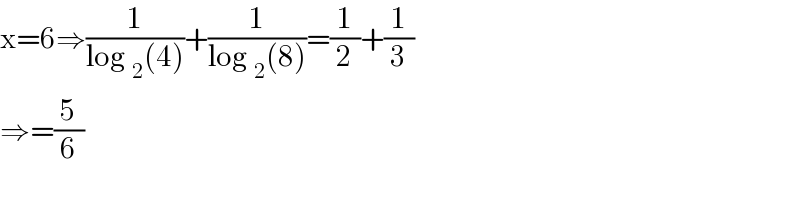
$$\mathrm{x}=\mathrm{6}\Rightarrow\frac{\mathrm{1}}{\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{4}\right)}+\frac{\mathrm{1}}{\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{8}\right)}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow=\frac{\mathrm{5}}{\mathrm{6}} \\ $$
Commented by mokys last updated on 18/Mar/23
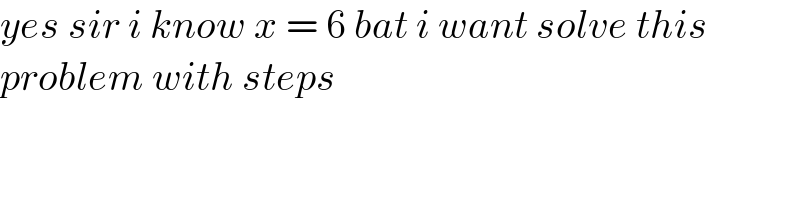
$${yes}\:{sir}\:{i}\:{know}\:{x}\:=\:\mathrm{6}\:{bat}\:{i}\:{want}\:{solve}\:{this}\: \\ $$$${problem}\:{with}\:{steps} \\ $$
Commented by mr W last updated on 19/Mar/23

$${there}\:{is}\:{no}\:{general}\:{method}\:{you}\:{can} \\ $$$${follow}\:{step}\:{by}\:{step}\:{to}\:{get}\:{the}\:{solution}. \\ $$$${in}\:{current}\:{special}\:{case}\:{you}\:{can}\:{only} \\ $$$$“{see}''\:{the}\:{solution}\:{x}=\mathrm{6}. \\ $$$${if}\:{the}\:{question}\:{is}\:{for}\:{example} \\ $$$$\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{2}} \:\left({x}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{2}} \:\left({x}+\mathrm{2}\right)^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{14}} \\ $$$${you}\:{can}\:{not}\:“{see}''\:{the}\:{solution}\:{any}\: \\ $$$${more}\:{and}\:{you}\:{can}\:{also}\:{not}\:{get}\:{the}\: \\ $$$${solution}\:{otherwise}.\:{you}\:{can}\:{only} \\ $$$${approximate}. \\ $$
Commented by Frix last updated on 18/Mar/23
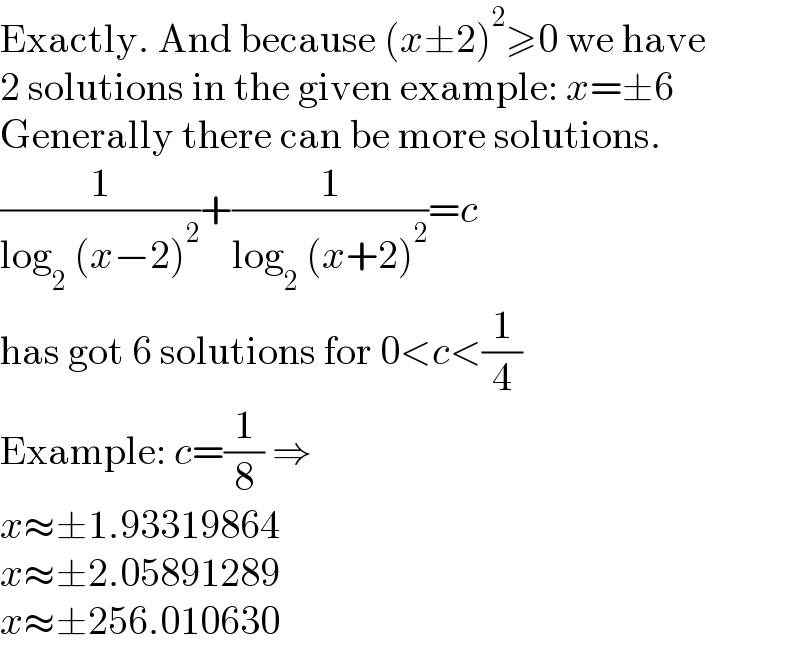
$$\mathrm{Exactly}.\:\mathrm{And}\:\mathrm{because}\:\left({x}\pm\mathrm{2}\right)^{\mathrm{2}} \geqslant\mathrm{0}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{2}\:\mathrm{solutions}\:\mathrm{in}\:\mathrm{the}\:\mathrm{given}\:\mathrm{example}:\:{x}=\pm\mathrm{6} \\ $$$$\mathrm{Generally}\:\mathrm{there}\:\mathrm{can}\:\mathrm{be}\:\mathrm{more}\:\mathrm{solutions}. \\ $$$$\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{2}} \:\left({x}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{2}} \:\left({x}+\mathrm{2}\right)^{\mathrm{2}} }={c} \\ $$$$\mathrm{has}\:\mathrm{got}\:\mathrm{6}\:\mathrm{solutions}\:\mathrm{for}\:\mathrm{0}<{c}<\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{Example}:\:{c}=\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow \\ $$$${x}\approx\pm\mathrm{1}.\mathrm{93319864} \\ $$$${x}\approx\pm\mathrm{2}.\mathrm{05891289} \\ $$$${x}\approx\pm\mathrm{256}.\mathrm{010630} \\ $$
Answered by kapoorshah last updated on 18/Mar/23
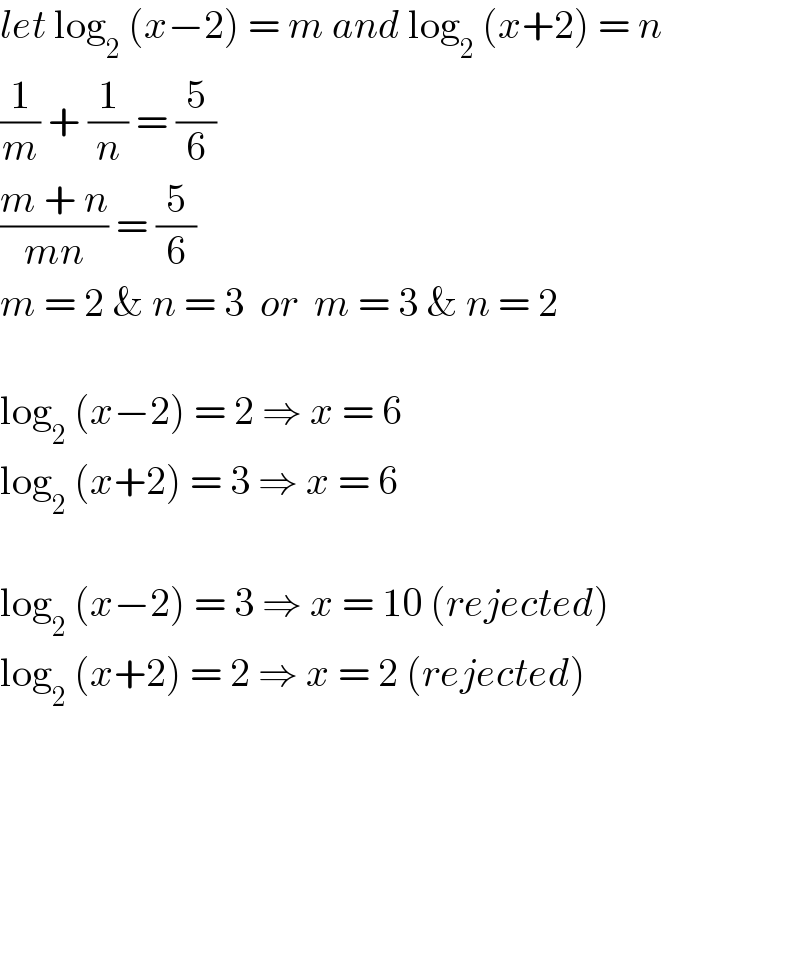
$${let}\:\mathrm{log}_{\mathrm{2}} \:\left({x}−\mathrm{2}\right)\:=\:{m}\:{and}\:\mathrm{log}_{\mathrm{2}} \:\left({x}+\mathrm{2}\right)\:=\:{n} \\ $$$$\frac{\mathrm{1}}{{m}}\:+\:\frac{\mathrm{1}}{{n}}\:=\:\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\frac{{m}\:+\:{n}}{{mn}}\:=\:\frac{\mathrm{5}}{\mathrm{6}} \\ $$$${m}\:=\:\mathrm{2}\:\&\:{n}\:=\:\mathrm{3}\:\:{or}\:\:{m}\:=\:\mathrm{3}\:\&\:{n}\:=\:\mathrm{2} \\ $$$$ \\ $$$$\mathrm{log}_{\mathrm{2}} \:\left({x}−\mathrm{2}\right)\:=\:\mathrm{2}\:\Rightarrow\:{x}\:=\:\mathrm{6} \\ $$$$\mathrm{log}_{\mathrm{2}} \:\left({x}+\mathrm{2}\right)\:=\:\mathrm{3}\:\Rightarrow\:{x}\:=\:\mathrm{6} \\ $$$$ \\ $$$$\mathrm{log}_{\mathrm{2}} \:\left({x}−\mathrm{2}\right)\:=\:\mathrm{3}\:\Rightarrow\:{x}\:=\:\mathrm{10}\:\left({rejected}\right) \\ $$$$\mathrm{log}_{\mathrm{2}} \:\left({x}+\mathrm{2}\right)\:=\:\mathrm{2}\:\Rightarrow\:{x}\:=\:\mathrm{2}\:\left({rejected}\right) \\ $$$$ \\ $$$$ \\ $$$$\: \\ $$$$ \\ $$$$ \\ $$
Commented by Frix last updated on 18/Mar/23
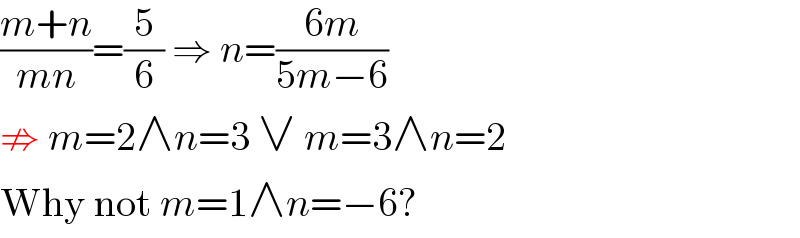
$$\frac{{m}+{n}}{{mn}}=\frac{\mathrm{5}}{\mathrm{6}}\:\Rightarrow\:{n}=\frac{\mathrm{6}{m}}{\mathrm{5}{m}−\mathrm{6}} \\ $$$$\nRightarrow\:{m}=\mathrm{2}\wedge{n}=\mathrm{3}\:\vee\:{m}=\mathrm{3}\wedge{n}=\mathrm{2} \\ $$$$\mathrm{Why}\:\mathrm{not}\:{m}=\mathrm{1}\wedge{n}=−\mathrm{6}? \\ $$
Commented by kapoorshah last updated on 18/Mar/23

$${m}\:=\:\mathrm{1}\: \\ $$$$\mathrm{log}_{\mathrm{2}} \:\left({x}−\mathrm{2}\right)\:=\:\mathrm{1}\:\Rightarrow\:{x}\:=\:\mathrm{4} \\ $$$${substitute}\:{x}\:=\:\mathrm{4}\:{to}\:{the}\:{equation} \\ $$$${LHS}\:\neq\:{RHS} \\ $$$$ \\ $$$$\mathrm{log}_{\mathrm{2}} \:\left({x}+\mathrm{2}\right)\:=\:\mathrm{1}\:\Rightarrow\:{x}\:=\:\mathrm{0} \\ $$$${substitute}\:{x}\:=\:\mathrm{0}\:{to}\:{the}\:{equation} \\ $$$${LHS}\:\neq\:{RHS} \\ $$$$ \\ $$$$\mathrm{log}_{\mathrm{2}} \:\left({x}−\mathrm{2}\right)\:=\:−\mathrm{6} \\ $$$$………………\:{LHS}\:\neq\:{RHS} \\ $$$$\mathrm{log}_{\mathrm{2}} \:\left({x}+\mathrm{2}\right)\:=\:−\mathrm{6} \\ $$$$………………\:{LHS}\:\neq\:{RHS} \\ $$$$ \\ $$$$ \\ $$
Commented by Frix last updated on 18/Mar/23
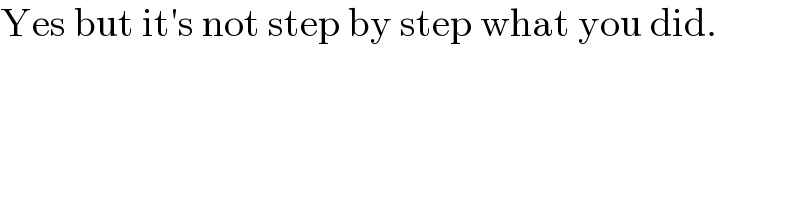
$$\mathrm{Yes}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step}\:\mathrm{what}\:\mathrm{you}\:\mathrm{did}. \\ $$
Commented by Frix last updated on 18/Mar/23

$$…\mathrm{your}\:\mathrm{method}\:\mathrm{is}\:\mathrm{wrong}.\:\mathrm{What}\:\mathrm{if}\:\mathrm{it}\:\mathrm{would} \\ $$$$\mathrm{be}\:\frac{{m}\:+\:{n}}{{mn}}=\frac{\mathrm{7}}{\mathrm{12}},\:\mathrm{would}\:\mathrm{you}\:\mathrm{get}\:{m}=\mathrm{3}\wedge{n}=\mathrm{4} \\ $$$$\mathrm{or}\:{m}=\mathrm{4}\wedge{n}=\mathrm{3}? \\ $$
Commented by kapoorshah last updated on 19/Mar/23
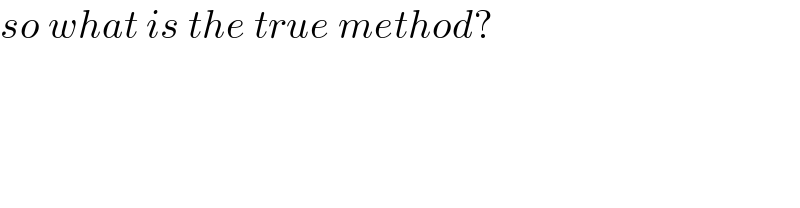
$${so}\:{what}\:{is}\:{the}\:{true}\:{method}? \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 19/Mar/23

$${it}\:{is}\:{said}\:{above}: \\ $$$${there}\:{is}\:{no}\:{general}\:{method}\:{you}\:{can} \\ $$$${follow}\:{step}\:{by}\:{step}\:{to}\:{get}\:{the}\:{solution}. \\ $$$${in}\:{current}\:{special}\:{case}\:{you}\:{can}\:{only} \\ $$$$“{see}''\:{the}\:{solution}\:{x}=\mathrm{6}. \\ $$$${if}\:{the}\:{question}\:{is}\:{for}\:{example} \\ $$$$\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{2}} \:\left({x}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{2}} \:\left({x}+\mathrm{2}\right)^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{14}} \\ $$$${you}\:{can}\:{not}\:“{see}''\:{the}\:{solution}\:{any}\: \\ $$$${more}\:{and}\:{you}\:{can}\:{also}\:{not}\:{get}\:{the}\: \\ $$$${solution}\:{otherwise}.\:{you}\:{can}\:{only} \\ $$$${approximate}. \\ $$
Answered by manxsol last updated on 19/Mar/23

$${a}={log}_{\mathrm{2}} \left({x}−\mathrm{2}\right) \\ $$$${b}={log}_{\mathrm{2}} \left({x}+\mathrm{2}\right) \\ $$$$\mathrm{2}^{{a}} ={x}−\mathrm{2} \\ $$$$\mathrm{2}^{{b}} ={x}+\mathrm{2} \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\mathrm{2}^{{b}} −\mathrm{2}^{{a}} =\mathrm{4}\:\:\:\: \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$${razonamiento}\:\:{tienen}\:{que} \\ $$$$\:{ser}\:{diferencias}\:{enteras}.{no} \\ $$$${existen}\:{otras}\:{soluciones} \\ $$$${porque}\:{seria}\:{irracional}={entero} \\ $$$${a}={b}−\mathrm{1} \\ $$$$\mathrm{2}^{{b}} −\frac{\mathrm{2}^{{b}} }{\mathrm{2}}=\mathrm{4} \\ $$$$\mathrm{2}^{{b}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{4} \\ $$$$\mathrm{2}^{{b}} =\mathrm{8} \\ $$$${b}=\mathrm{3} \\ $$$$\mathrm{3}={log}_{\mathrm{2}} \left({x}+\mathrm{2}\right) \\ $$$$\mathrm{8}={x}+\mathrm{2} \\ $$$${x}=\mathrm{6} \\ $$$$ \\ $$$$ \\ $$
Commented by manxsol last updated on 19/Mar/23
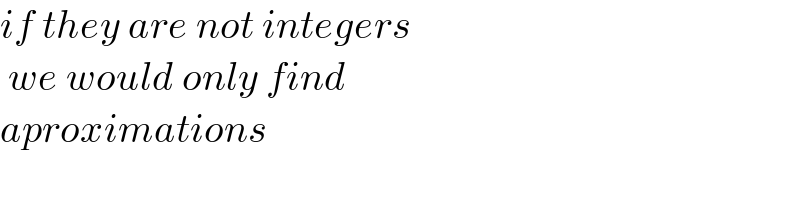
$${if}\:{they}\:{are}\:{not}\:{integers} \\ $$$$\:{we}\:{would}\:{only}\:{find}\: \\ $$$${aproximations} \\ $$
Commented by mr W last updated on 19/Mar/23
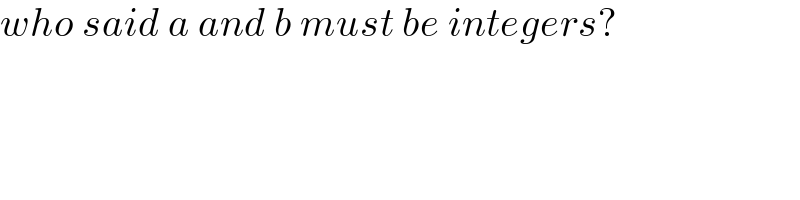
$${who}\:{said}\:{a}\:{and}\:{b}\:{must}\:{be}\:{integers}? \\ $$
