Question Number 189616 by Rupesh123 last updated on 19/Mar/23
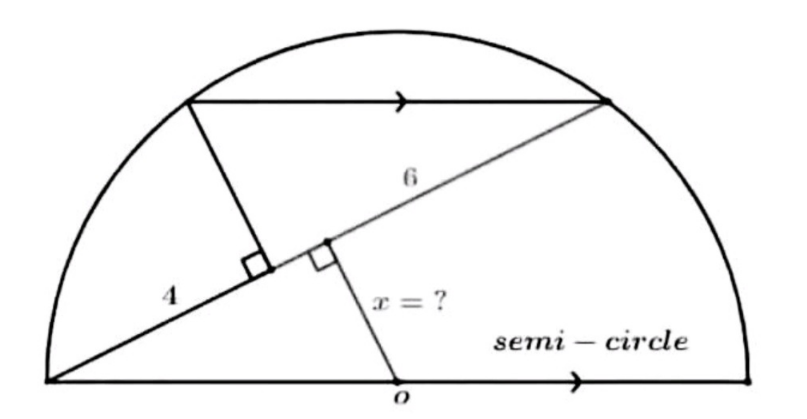
Answered by HeferH last updated on 19/Mar/23

Commented by HeferH last updated on 19/Mar/23

$$\:\mathrm{say}\:\mathrm{r}\:=\:\mathrm{5m} \\ $$$$\:\mathrm{m}\left(\mathrm{5m}\right)\:=\:\left(\mathrm{5m}−\mathrm{2x}\right)\left(\mathrm{5m}+\mathrm{2x}\right) \\ $$$$\:\mathrm{5m}^{\mathrm{2}} =\mathrm{25m}^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} \\ $$$$\mathrm{4x}^{\mathrm{2}} =\mathrm{20m}^{\mathrm{2}} \\ $$$$\:\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{5m}^{\mathrm{2}} \\ $$$$\:\mathrm{5m}^{\mathrm{2}} +\mathrm{25}\:=\:\mathrm{25m}^{\mathrm{2}} \\ $$$$\:\mathrm{25}\:=\:\mathrm{20m}^{\mathrm{2}} \\ $$$$\:\mathrm{m}^{\mathrm{2}} \:=\:\frac{\mathrm{25}}{\mathrm{20}}\:=\:\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\:\mathrm{x}^{\mathrm{2}} \:=\:\frac{\mathrm{25}}{\mathrm{4}}\:\Rightarrow\:\mathrm{x}\:=\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$
Commented by Rupesh123 last updated on 19/Mar/23
Nice solution, sir!
